To Be Filled or Not to Be Filled

Geometry Level 3

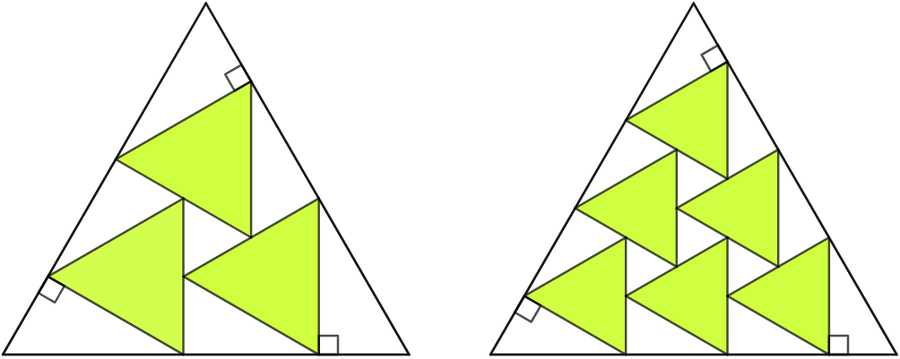
The unit equilateral triangle on the left inscribes two rows of similarly positioned tangential equilateral triangles, such that their sides are perpendicular to the outer perimeter.

The unit equilateral triangle on the right inscribes three rows of similarly positioned tangential equilateral triangles, where only three of them are tangent to four triangles.

If that pattern continues in the row sequence of $3, 6, 10, 15, \dots$ identical triangles, what is the area ratio of the shaded area to the area of the large triangle for infinite number of rows?

\dfrac{1}{2}

\dfrac{2}{3}

\dfrac{3}{4}

\dfrac{4}{5}

\dfrac{5}{6}

\dfrac{7}{8}

1

None of the given choices

1 solution

David Vreken
Mar 25, 2021

Let there be $n$ green equilateral triangles along the bottom row, and let each green equilateral triangle have a side of $x$ . Then using the ratios from the $30$ - $60$ - $90$ triangle, the left segment along the bottom is $\cfrac{2\sqrt{3}}{3}x$ , the right segment along the bottom is $\cfrac{\sqrt{3}}{3}x$ , and the segments in between are $\cfrac{\sqrt{3}}{2}x$ .

From the sum of bottom segment, $\cfrac{2\sqrt{3}}{3}x + (n - 1)\cfrac{\sqrt{3}}{2}x + \cfrac{\sqrt{3}}{3}x = 1$ , which solves to $x = \cfrac{2}{(n + 1)\sqrt{3}}$ .

There are $\cfrac{n(n + 1)}{2}$ green equilateral triangles for a total area of $A_{\text{green}} = \cfrac{n(n + 1)}{2} \cdot \cfrac{\sqrt{3}}{4}x^2 = \cfrac{n(n + 1)}{2} \cdot \cfrac{\sqrt{3}}{4}\bigg(\cfrac{2}{(n + 1)\sqrt{3}}\bigg)^2 = \cfrac{\sqrt{3}}{4} \cdot \cfrac{2n}{3n + 3}$ .

Since the large triangle has an area of $A_{\text{large}} = \cfrac{\sqrt{3}}{4} \cdot 1^2 = \cfrac{\sqrt{3}}{4}$ , the ratio of the shaded area to the area of the large triangle is $\cfrac{A_{\text{green}}}{A_{\text{large}}} = \cfrac{2n}{3n + 3}$ .

Therefore, for an infinite number of rows, the ratio is $\displaystyle \lim_{x\to\infty} \cfrac{2n}{3n + 3} = \boxed{\cfrac{2}{3}}$ .

To Be Filled or Not to Be Filled

1 solution

0 pending reports