To enjoy the geometra 2
The figure shows a semicircle inside a right triangle ABC at C . the semi-circle has its diameter on the hypotenuse AB and the lines AC and BC are tangential to the semicircle , the angle CAB = . AB = 30 Units. If the area Inside The Triangle ABC and outside the semicircle is A , Then
= ?
Hint : The first step is to find the radius of The Semicircle.
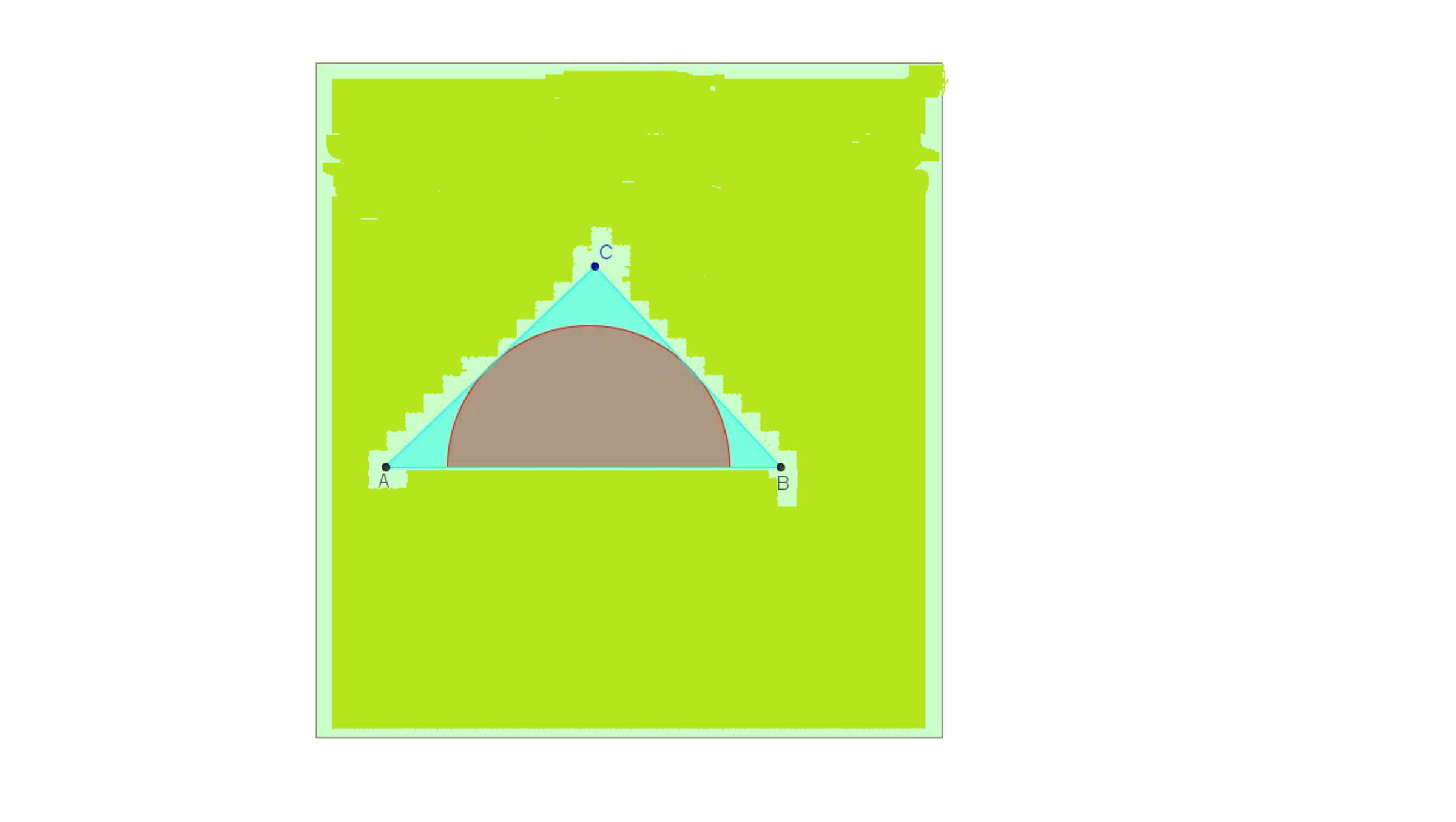
The answer is 225.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
let the coordinates of A be ( 0,0) and B = (30,0) then C = ( 22.5,7.5√3). and let the coordinates of O = (a,0).
Then the slope of CO = tan75 = 2 + √3 = 2 2 . 5 − a 7 . 5 √ 3 , then a = 3 4 5 ( 3 − √ 3 ) = 15(3 - √3).
The equations of the lines AC and HO are :
Y = √ 3 x , y = -√3(x-a) respectively , Solving simultaneously the coordinates of H = (x,y) in terms of a can be ;
The coordinats of H = ( 4 3 a , 4 √ 3 a )
and O = (a,0).
Then OH = R = √ ( 1 6 a 2 + 1 6 3 a 2 ) = 2 a = 2 1 5 ( 3 − √ 3 )
Then :
A = (15²√3)/2 – π/2 ( 15/2)² (3 - √3)² , 4A = (15)²(2√3 - 6π + 3√3).
ANSWER = 15² = 225.