To Equal or Not To Equal
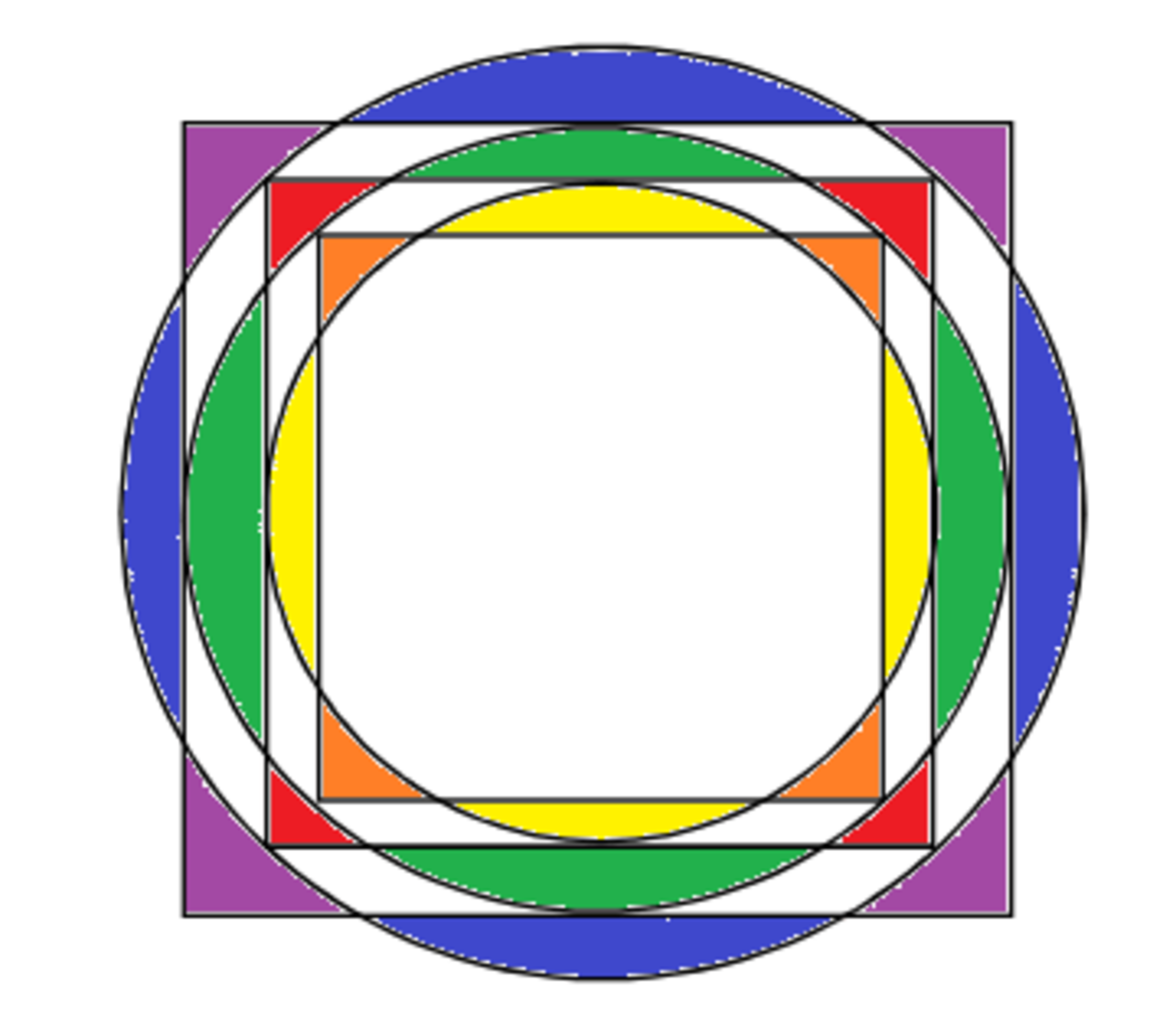
The blue and purple areas are equal to each other. Each internal circle is inscribed in a square, and each internal square is inscribed in a circle. Which of the following statements are true?
A: The red and green areas are equal to each other.
B: The orange and yellow areas are equal to each other.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For the purple and blue areas to have the same extent, the area of the outermost square has to be equal to the area of the outermost circle. If the radius of that circle R 1 = 1 , the circle has area A c 1 = π , and the side of the square, x 1 = π .
The next circle has a radius R 2 = 2 x 1 = 2 π and area A c 2 = π × 4 π = 4 π 2 ≈ 2 . 4 7 . The square to go with it has a side x 2 = 2 × R 1 = 2 and area A s 2 = 2 . These areas are not equal and statement A is false.
Then innermost circle has a radius R 3 = 2 x 2 = 2 1 and area A c 3 = 2 π . The innermost square has a side x 3 = 2 × R 2 = 2 π and area A s 3 = 2 π . These two areas are the same and statement B is true.
...
Basically to go from R 1 to R 3 we multiply by 2 and divide by 2 .
To go from x 1 to x 3 we divide by 2 and multiply by 2 .
Both operations result in a net division by 2 , so if the first set of dimensions resulted in equal areas, so will the last set, and the areas will be half of what we started with. There is no reason for the intermediate figures to have the same area, and they don't.