To Infinity and Beyond!

Geometry Level 3

Imagine n n squares each of side x x lined up as shown in the picture. You are to draw a line connecting the top corner of the first square to the bottom corner of each square. The case n = 3 n=3 is shown as follows.

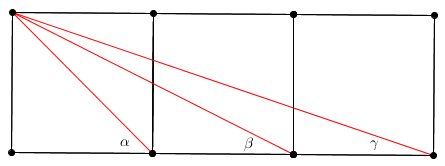
Define S n S_n as the sum of all angles, in radians, formed by the lines you have constructed for n n squares. S 3 = α + β + γ = π 2 S_3= \alpha+\beta+\gamma=\frac{\pi}{2} for example.

What is lim ⁡ n → ∞ S n \displaystyle \lim_{n\to \infty}{S_n} ?

Can not be calculated without the value of x x π 2 6 \frac{\pi^2}{6} π 2 \pi^2 The limit diverges π ln ⁡ π \pi \ln{\pi}

Hamza A by Hamza A , 19, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Hamza A
Dec 28, 2018

Angle α = arctan ⁡ ( x x ) = arctan ⁡ 1 \alpha=\arctan{\left( \frac{x}{x} \right)}=\arctan{1}

Angle β = arctan ⁡ ( x 2 x ) = arctan ⁡ 1 2 \beta=\arctan{\left( \frac{x}{2x} \right)}=\arctan{\frac{1}{2}}

Angle γ = arctan ⁡ ( x 3 x ) = arctan ⁡ 1 3 \gamma=\arctan{\left( \frac{x}{3x} \right)}=\arctan{\frac{1}{3}}

We see a pattern here. S n = arctan ⁡ 1 1 + arctan ⁡ 1 2 + arctan ⁡ 1 3 . . . + arctan ⁡ 1 n S_n=\arctan{\frac{1}{1}}+\arctan{\frac{1}{2}}+\arctan{\frac{1}{3}} ... \ \ +\arctan{\frac{1}{n}}

Therefore, S n = ∑ k = 1 n arctan ⁡ ( 1 k ) S_n=\displaystyle \sum_{k=1}^{n}{\arctan{\left( \frac{1}{k} \right)}} .

The series ∑ k = 1 ∞ arctan ⁡ ( 1 k ) \displaystyle \sum_{k=1}^{\infty}{\arctan{\left( \frac{1}{k} \right)}} diverges by comparison. Hence, lim ⁡ n → ∞ S n \displaystyle \lim_{n\to \infty}{S_n} diverges

3 Helpful 3 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...