To infinity and beyond
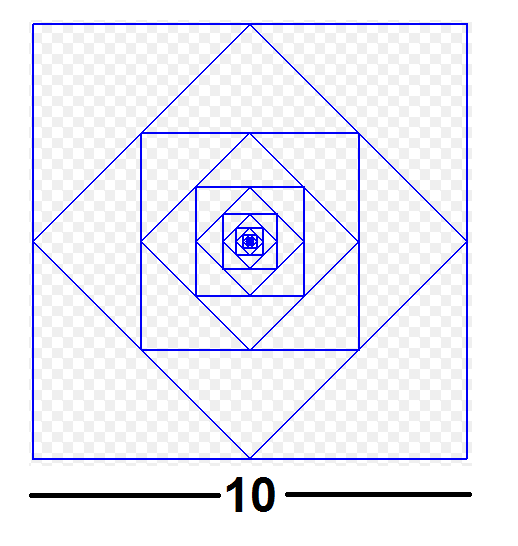 The given figure shows a square of side 10 units. Joining the midpoints of its sides, another square is drawn in it.
The given figure shows a square of side 10 units. Joining the midpoints of its sides, another square is drawn in it.
This process is continued forever.
What is the sum of areas of all the squares?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If you observe the figure properly , you can see that the area of each square is 1/2 times of the area of the previous square.
Let area of the larger square be A
Clearly the sum of the areas will be a GP like this :
S + 2 S + 4 S + . . . . .
i.e,
S × ( 1 + 2 1 + 4 1 + . . . . . )
Now, the formula for infinite series of GP can be used
S × 1 − 2 1 1
Which is nothing but ,
2 × S
Area of larger square S is,
S = 1 0 × 1 0 = 1 0 0
∴ Sum of the area of all the squares is,
2 × 1 0 0 = 2 0 0