To Infinity (but not beyond)
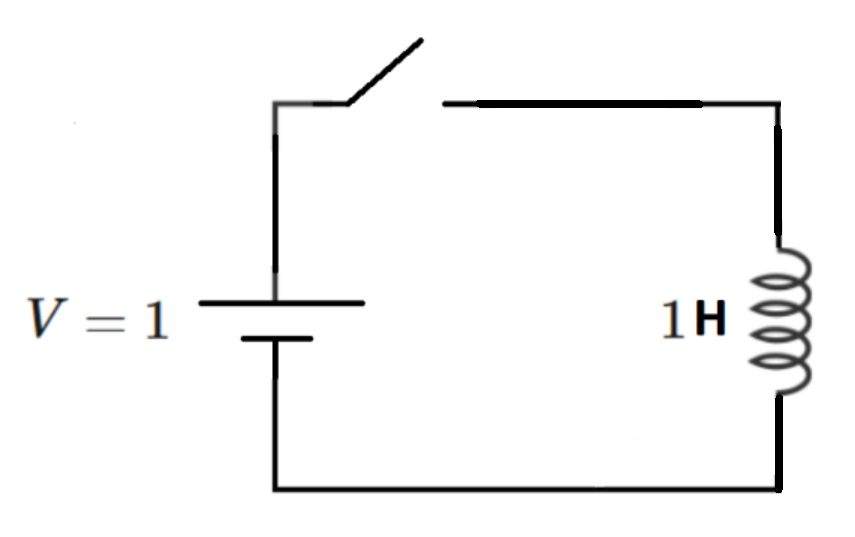
An ideal inductor is excited by an ideal DC voltage source through a switch, which is initially open. The inductor is initially de-energized. The switch closes at time .
At time , what is the current through the inductor?
The answer is 8675309.0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The inductor current ramp rate is proportional to the applied voltage. If the voltage is constant, so is the current ramp rate. Since V = 1 V and L = 1 H , the ramp rate is L V = d t d I = 1 A ⋅ s − 1 → I = I 0 + ( A ⋅ s − 1 ) t
(Assuming t is in seconds . . . MKS/SI units and all.)
Plug in the time t = 8 6 7 5 3 0 9 s and we have the answer as 8 6 7 5 3 0 9 A .
Note: In real life, you would fry the battery or power source before you can get this kind of current.