To Iterate or Not to Iterate? (Part 3)

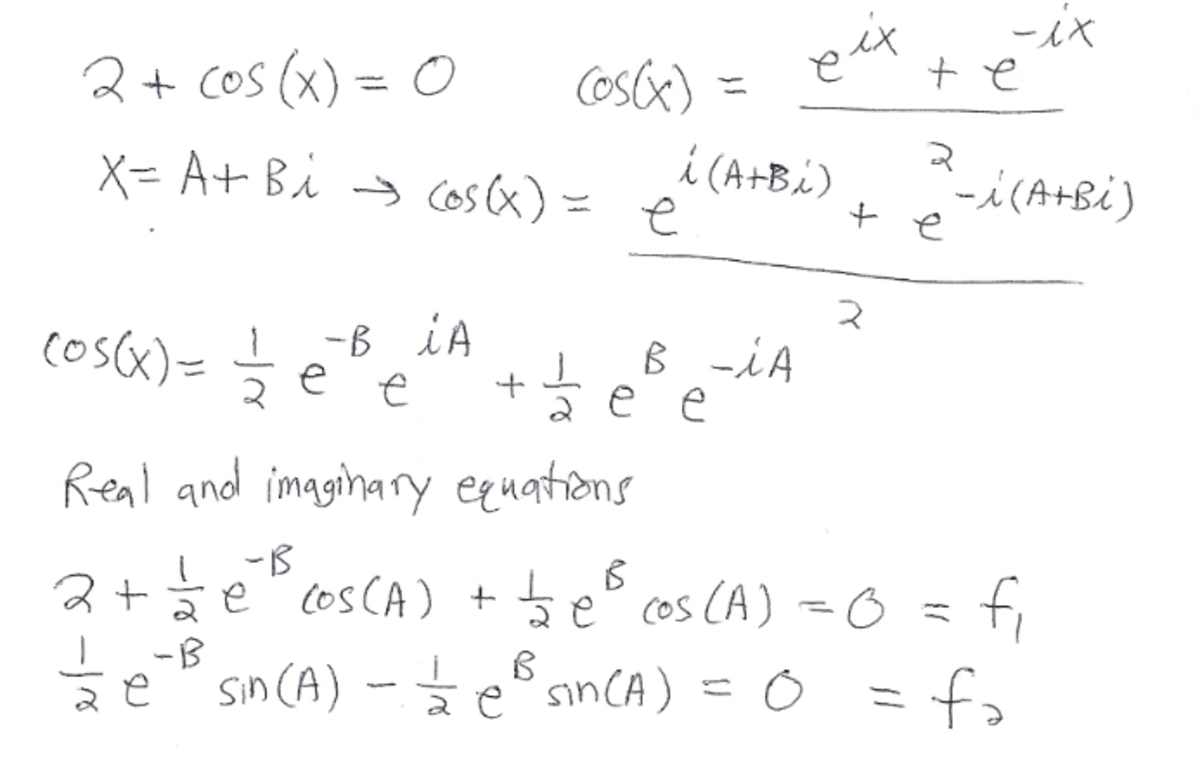
It's possible to get an exact solution. I will denote the imaginay unit as $j$ since I am an electronical engineer =D

$\frac{ e^{(j\cdot(a + jb))} + e^{(-j\cdot(a + jb))}}{2} + 2 = 0$

$e^{(ja -b )} + e^{(-ja + b )} = -4$

$e^{-b}\cdot(cos(a) + j\cdot sin(a) ) + e^b \cdot (cos(a) - j\cdot sin(a)) = -4$

Separating real and imaginary equations:

$(i)$ $cos(a)\cdot(e^b + e^{-b}) = -4$

$(ii)$ $sin(a)\cdot(e^{-b} - e^b) = 0$

From $(ii)$ , either $e^b = e^{-b}$ , which will lead to $b=0$ or $sin(a) = 0$ , which will lead to $a = k\pi, k \in \mathbb{Z}$

Pluggin $b = 0$ in $(i)$ we will have $cos(a) = -2$ , which have no solution for real $a$ . Hence, $a = k\pi$ . Pluggin this in $(i)$ :

$(-1)^k \cdot (e^b + e^{-b}) = -4$

Or:

$(e^b + e^{-b}) = -4$ $(k$ $even)$

$(e^b + e^{-b}) = 4$ $(k$ $odd)$

Since both $e^b$ and $e^{-b}$ are greater than 0, the first equation cannot be true. Hence, $k$ is odd and in order to $\sqrt{a^2 + b^2}$ to be minimum, $a$ should be equal to $\pm \pi$

Substituting $e^b$ as $y$ in the second equation, we will have $y^2 - 4y + 1 = 0$ , or $y = 2 \pm \sqrt{3}$

Hence, b will be equal to $ln(2 \pm \sqrt{3}) = \pm \fbox{1.317... }$

Substituing $a$ as $\pm \pi$ and $b$ as $\pm 1.317...$ we have $\sqrt{a^2 + b^2} = \fbox{3.406...}$

I used the multivariate Newton Raphson method, as in Parts 1 and 2. The Jacobian derivation is given below. The "minimum" solutions come out to be $(\pm\pi\pm1.317i)$ , which all have a magnitude of approximately 3.406.