To Pump or Not to Pump?
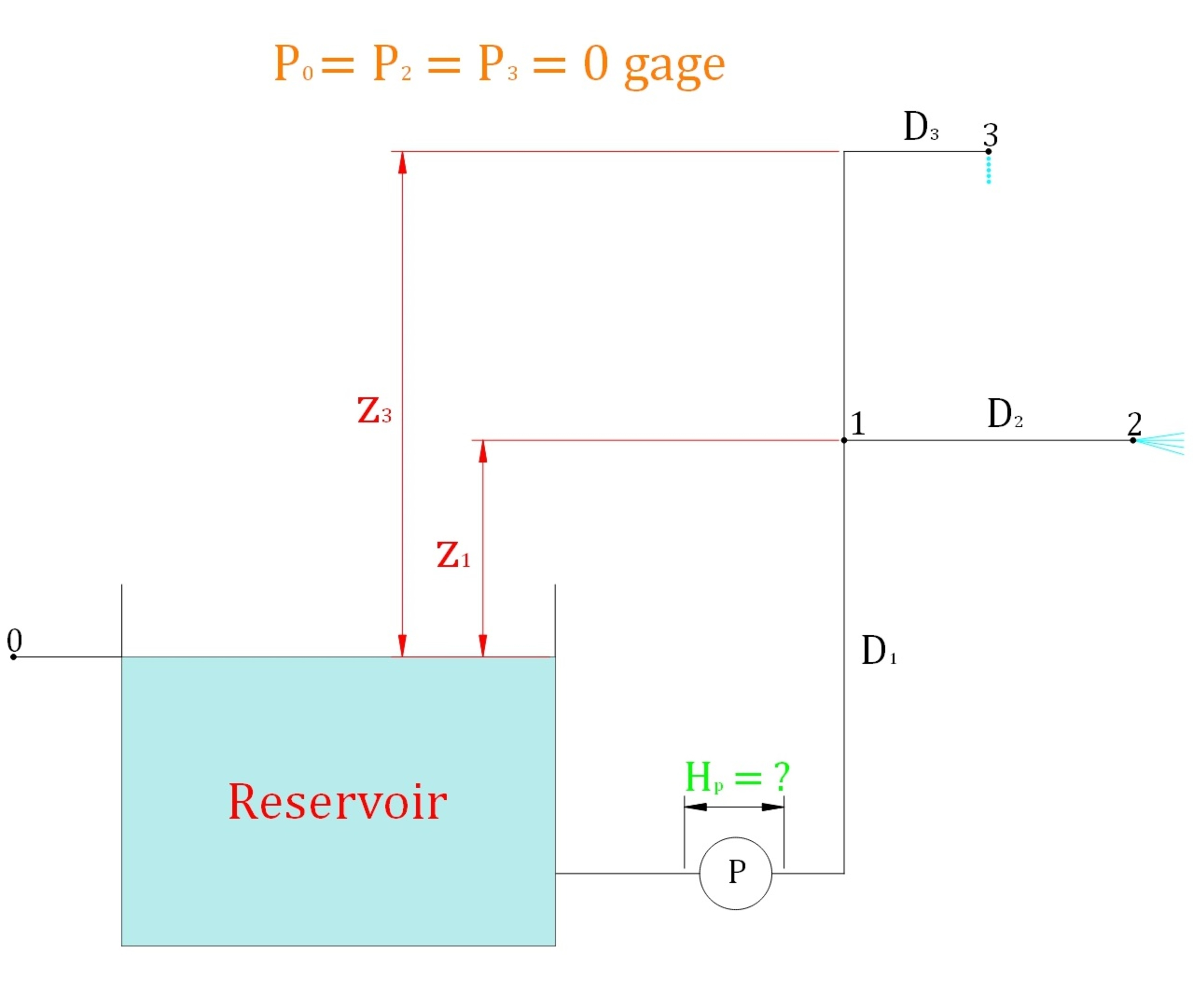
What is the minimum pump head ( H p ) required by the system in [ ft ] to initiate flow at point "3" in the piping system above?
P r o b l e m I n f o r m a t i o n :
Conservation of Energy derived flow model applied between points "a" and "b" in the system:
ρ g P a + z a + α 2 g v a 2 + H p = ρ g P b + z b + α 2 g v b 2 + ∑ h l a − b
P 0 = P 2 = P 3 = 0 gage ( Ambient Pressure at points 0, 2 & 3, respectively)
z 1 = z 2 = 1 0 [ ft ] (Static Elevation)
z 3 = 5 0 . 5 [ ft ] (Static Elevation)
D 1 = 1 . 5 [ in ] (Interior Pipe Diameter - Section "0 to 1")
D 2 = D 3 = 1 [ in ] ( Interior Pipe Diameter - Sections "1 to 2" & "1 to 3", respectively)
K 0 − 1 = 5 ( Effective Loss Coefficient - Section "0 to 1")
K 1 − 2 = K 1 − 3 = 3 ( Effective Loss Coefficient - Section "1 to 2" & "1 to 3", respectively)
The reservoir is taken to be very large; as such its depth remains approximately constant, and the kinetic head at point "0" is to be neglected.
All flows are assumed incompressible, turbulent (kinetic head correction factor α = 1 ), irrotational, and viscous. Thermal losses (head loss for piping and fittings in any portion of the system) are to be modeled as follows:
h l a − b [ ft ] = 2 g K a − b v a − b 2
where,
K a − b is the effective loss coefficient (taken to be exact) for the transmission of flow between points "a" and "b" in the piping system, and v a − b is the average velocity of that flow for a given pipe diameter D i .
The answer is 60.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Applying Conservation of Energy in a suitable form for fluids systems (Energy per unit Weight):
S e c t i o n 0 - 1
γ P 0 + z 0 + α 2 g v 0 2 + H p = γ P 1 + z 1 + α 2 g v 1 2 + ∑ h l 0 − 1
Begin by simplifying the expression and substitute in the relation for head loss in the problem statement, solve for H p : P 0 = 0 gage , z 0 = 0 , v 0 ≈ 0 , α = 1
H p = γ P 1 + z 1 + 2 g v 1 2 + K 0 − 1 2 g v 1 2 ...EQ1
S e c t i o n 1 - 2
This is the same analysis as above applied between points 1 and 2 with: H p = 0 , z 1 = z 2 , P 2 = 0 gage . A goal is to eliminate γ P 1 from EQ1, solving for it:
γ P 1 = 2 g v 2 2 ( 1 + K 0 − 1 ) − 2 g v 1 2 ...EQ2
S e c t i o n 1 - 3
Same application as above between points 1 and 3 with, H p = 0 , P 3 = 0 gage and the criteria v 3 = 0 , we find:
γ P 1 = ( z 3 − z 1 ) − 2 g v 1 2 ...EQ3
Now we can substite EQ3 into EQ1, eliminating γ P 1 and simplify, finding:
H p = z 3 + K 0 − 1 2 g v 1 2 ...EQ1'
Assuming the velocity profile is approximately constant across the pipes, we can derrive the velocity of the flow in terms of the volumetric flow rate using the cross sectional area A 1 :
Q 1 = v 1 A 1 ...EQ4
Rearrange EQ4 for v 1 and sub into EQ1':
H p = z 3 + K 0 − 1 A 1 2 2 g Q 1 2 ...EQ1''
Furthermore, we may apply continuity ( conservation of mass for incompressible flows) at point 1:
Q 1 = Q 2 + Q 3 ...EQ5
Letting Q 3 go to zero:
Q 1 = Q 2
It then follows that:
H p = z 3 + K 0 − 1 A 1 2 2 g Q 2 2 ...EQ1'''
Now, since Branch 1-2 & 1-3 are in parallel, they have a common pressure at point 1. We may equate EQ2 and EQ3 through the common pressure P 1 . ( v 3 = 0 already being accounted for in EQ3) we obtain ( solving for Q 2 2 in terms of v 2 , A 2 ) :
2 g v 2 2 ( 1 + K 0 − 1 ) − 2 g v 1 2 = ( z 3 − z 1 ) − 2 g v 1 2
→ Q 2 2 = 2 g A 2 2 1 + K 1 − 2 z 3 − z 1 ...EQ6
Finally, sub EQ6 into EQ1''', with A 1 A 2 = ( D 1 D 2 ) 2 :
H p = z 3 + 1 + K 1 − 2 K 0 − 1 ( D 1 D 2 ) 4 ( z 3 − z 1 ) = 5 0 . 5 [ ft ] + 1 + 3 5 ( 1 . 5 [ in ] 1 [ in ] ) 4 ( 5 0 . 5 [ ft ] − 1 0 [ ft ] ) = 6 0 . 5 [ ft ]
**Given a pump that outputs the required head, the system flow can be found from EQ6 to be approximately 6 2 . 5 [ gpm ] . Any further increase in head delivered by the pump and the criterion v 3 = 0 no longer holds. To determine head and flow state beyong H p a solution to a system of non-linear equations must be employed ( methods typically involve linearization and iteration)