Tomi's Challenges - #16

We are given that both $c(t)$ and $d(t)$ are closed curves and that $d(t)$ is the curve that results by transforming $c(t)$ by that matrix monstrosity. Since both curves have an area, we can use the determinant of the matrix to determine the scaling factor between $d(t)$ and $c(t)$ .

$\det{\begin{bmatrix} \sqrt[2021]{2 * 10^{100}} & 202120212021^{202120212021} \\ 0 & \sqrt[2021]{2 * 10^{100}} \end{bmatrix}^{2021}} = x^{2021}$ where $x = \det{\begin{bmatrix} \sqrt[2021]{2 * 10^{100}} & 202120212021^{202120212021} \\ 0 & \sqrt[2021]{2 * 10^{100}} \end{bmatrix}}$

Since the base matrix (the form of the matrix that is not raised to the 2021st power) is 2 x 2, calculating its determinant is relatively straightforward. $x = (\sqrt[2021]{2 * 10^{100}})(\sqrt[2021]{2 * 10^{100}}) - (202120212021^{202120212021})(0) = \sqrt[2021]{4 * 10^{200}}$ . To find the determinant of the base matrix raised to the 2021st power, we simply raise $x$ to the 2021st power. This cancels out the radical leaving us a determinant of $4 * 10^{200}$ .

To determine the area of $d(t)$ , we multiply the area of $c(t)$ by the determinant. This gives an area for $d(t)$ equal to $8084 * 10^{200} = 80840000...0$ . Therefore, the sum of the digits of the area of $d(t)$ is $8 + 0 + 8 + 4 + 200(0) = \boxed{20}$ .

This problem is kind of a harder version of Tomi's Challenges #1. The approach is similar, we need to figure out how the matrix changes the area of the curve $c$ . Let $A=\begin{bmatrix} \sqrt[2021]{2\cdot10^{100}} & 202120212021^{202120212021}\\ 0 & \sqrt[2021]{2\cdot10^{100}} \end{bmatrix}^{2021}$

We can write $A$ as:

$A=\left(\begin{bmatrix} \sqrt[2021]{2\cdot10^{100}} & 0\\ 0 & \sqrt[2021]{2\cdot10^{100}} \end{bmatrix}\begin{bmatrix} 1 & \frac{202120212021^{202120212021}}{\sqrt[2021]{2\cdot10^{100}}}\\ 0 & 1 \end{bmatrix}\right)^{2021}=$ (since both matrices commute) $\begin{bmatrix} \sqrt[2021]{2\cdot10^{100}} & 0\\ 0 & \sqrt[2021]{2\cdot10^{100}} \end{bmatrix}^{2021}\begin{bmatrix} 1 & \frac{202120212021^{202120212021}}{\sqrt[2021]{2\cdot10^{100}}}\\ 0 & 1 \end{bmatrix}^{2021}=\begin{bmatrix} 2\cdot10^{100} & 0\\ 0 & 2\cdot10^{100} \end{bmatrix}\begin{bmatrix} 1 & \frac{202120212021^{202120212021}}{\sqrt[2021]{2\cdot10^{100}}}\\ 0 & 1 \end{bmatrix}^{2021}$

The left matrix scales the curve uniformly $2\cdot10^{100}$ times. Its area is therefore increased $4\cdot10^{200}$ times. The right matrix is a tilt matrix which tilts the shape of the curve to the right by $\frac{202120212021^{202120212021}}{\sqrt[2021]{2\cdot10^{100}}}$ , $2021$ times. Let's look at what happens to for example a square when it gets tilted:

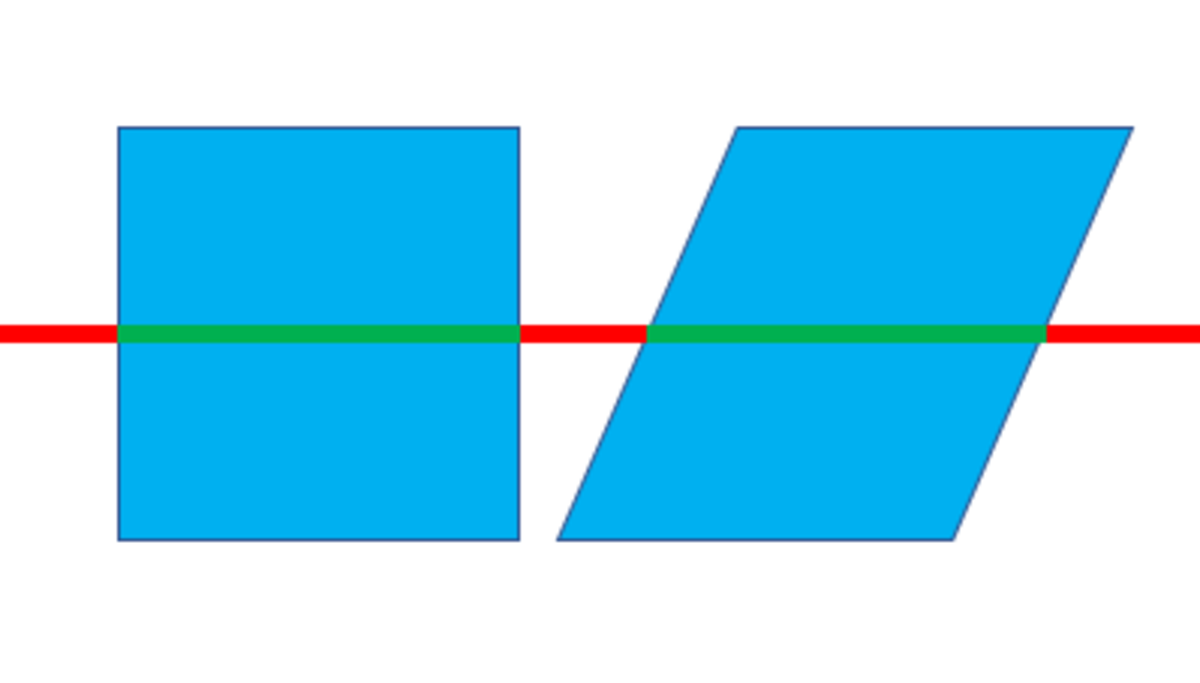
If we slice the square and paralellogram with the same horizontal line, we get that their width is the same. No matter where we intersect them with a horizontal plane, their width will always be the same. Therefore we can conclude that the same exact thing happens with curves, because tilting something is really just a way of rearranging the horizontal lines of a shape, in a homeomorphic way. By Cavalieri's principle , the original curve and the tilted curve have the same area. So therefore this matrix has no influence on the area, and the area of the new curve is therefore $2021\cdot4\cdot10^{200}$ , and the sum of its digits is 8+0+8+4+ a bunch of zeroes=20.