Too many vertical lines

Since the LHS is an even function, in suffices to consider $x\geq 0$ , by symmetry.

For $x\geq 1$ , the function $f(x)=2^x(x-1)$ is increasing to infinity, with $f(1)=0$ , so that there is exactly one solution, $c$ , by the intermediate value theorem.

For $0\leq x\leq 1$ , the function $g(x)=2^x(1-x)$ is decreasing (the derivative is negative), so that $g(0)=1$ is the only solution.

Thus we have $\boxed{3}$ solutions all together, $c, -c$ and 0.

Making a rough graph too would give the same results

Taking the natural logarithm on both sides of the given equation gives us

$(|x|\ln 2)(\ln|1-|x||) = 0$

which means that $|x| = 0$ or $\ln|1-|x|| = 0$ . It is clear that $|x| = 0$ if $x = 0$ , and that $\ln|1-|x|| = 0$ if $x = 0,2,-2$ , so our solution set is $\boxed{\{ 0,2,-2 \}}$ .

We can rewrite the original equation, according to the rules of logarithms, to ge the following: $\ln{\big|1-|x|\big|}=-|x|\ln{2}$

By using transformations of graphs, we can sketch a rough graph for the funcions on each side of the equation:

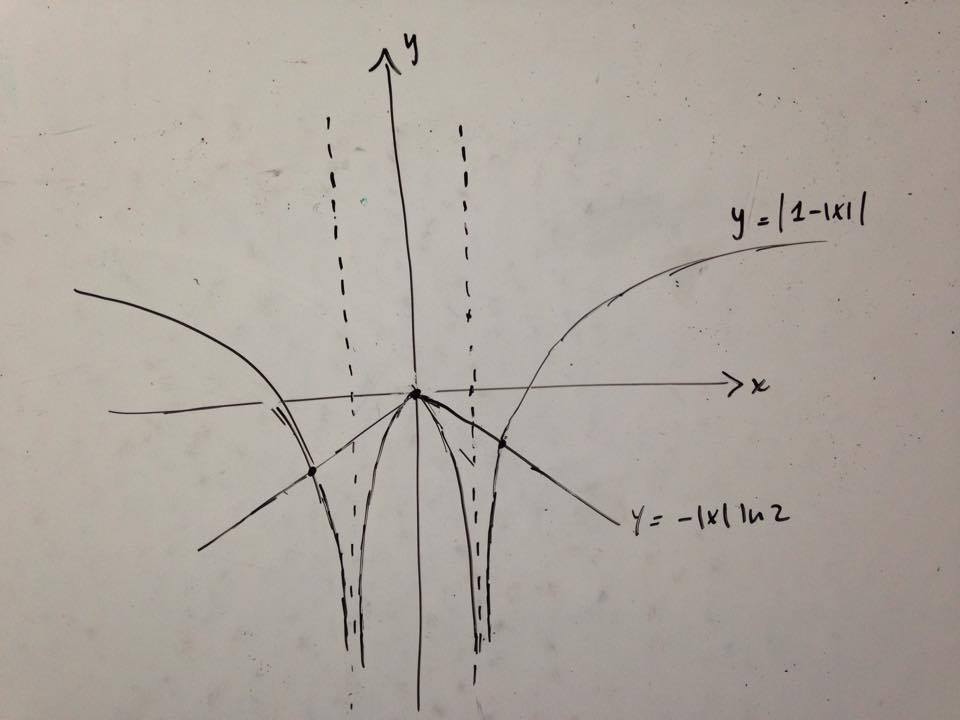
Here the number of intersections of both graphs gives the number of solutions. Now, for there to be more than 3 solutions (i.e. 5), we would require that the gradient of our line $y=-|x|\ln{2}$ is greater (in absolute value) than the gradient (in absolute value) of the tangent to $y=\ln{\big|1-|x|\big|}$ at the origin, which we can find to be 1 using calculus (assuming that the funcion is differentiable at this point). Since the gradient of our line is $\ln{2} < 1$ , we know that there's only 3 solutions to the equation.

Graph of 2^x and jigsaw pattern of 1-x will yield 3 intersections