A classical mechanics problem by rahul singh

Classical Mechanics Level 5

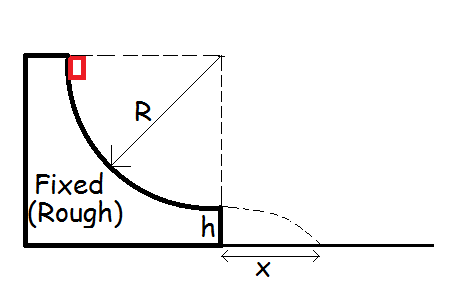
Consider a fixed wedge whose part is a quarter circle of radius R as shown. A small block of mass m slides down the wedge and leaves horizontally from a height h as shown. the coefficient of friction between wedge and block is k. compute the value of x in millimetres , where x is the distance from the bottom of the wedge of the point where the block falls given the values below:

Details - R = 200cm - h = 105 cm - k = 0.5 - m = 2g - Round your answer in centimetres to nearest integer and then enter it in millimetres

The answer is 890.

1 solution

Rahul Singh
Apr 30, 2017

First, we make the force diagram at the instant when then angle made by line joining center of circle, and block with horizontal is A . The force diagram would be as shown. Let the speed of the block at this instant be v. Clearly, there would be two components of acceleration , centripetal and tangential.

We know that centripetal acceleration is given by $\frac{v^2}{r}$ , hence we use Newton's law to get: N - mgsinA = $\frac{m(v^2)}{r}$

We know that , . f = kN

f = k(mgsinA + $\frac{m(v^2)}{r}$ )

Now, tangential acceleration = $\frac{dv}{dt}$ = $\frac{d(v^2)}{2rdA}$ , hence, using Newton's law,

mgcosA - k(mgsinA + $\frac{m(v^2)}{r}$ )= m $\frac{d(v^2)}{2rdA}$

Rearrange and divide by m to get: $\frac{d(v^2)}{dA}$ + 2k(v^2) = 2Rg(cosA - ksinA)

Clearly, this is a Linear Differential equation in A and .

Integrating factor = e^(2kA)

Solving, we get: x = 89cm = 890mm

Can you please explain how you got the tangential acceleration = $\frac{d(v^2)}{2r \ dA}$

Viraam Rao - 3 years, 5 months ago

tangential acc is dv/dt which can be rewritten as vdv/dr now here if u take proper components..and write 2vdv as d(v^2)..u will get the result

rahul singh - 3 years, 5 months ago

A classical mechanics problem by rahul singh

The answer is 890.

1 solution

0 pending reports