A Tricky Semicircle
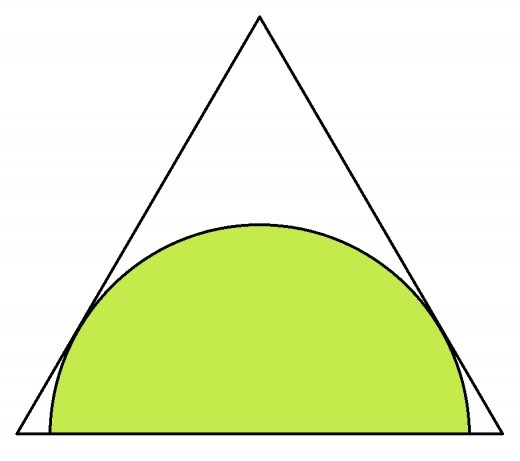
A semi-circle is inscribed within an equilateral triangle such that the diameter of the semi-circle is centered on one side of the triangle and the arc is tangent to the other two sides.
If each side of the triangle is of length 4 cm, then what is the diameter of the semi-circle (in cm)?
Give your answer to 3 decimal places.
The answer is 3.464.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
This is a solution using the principles of trigonometry. Good solution. In my solution , I used only Pythagorean Theorem.
 By pythagorean theorem,
A
E
=
4
2
−
2
2
=
1
6
−
4
=
1
2
By pythagorean theorem,
A
E
=
4
2
−
2
2
=
1
6
−
4
=
1
2
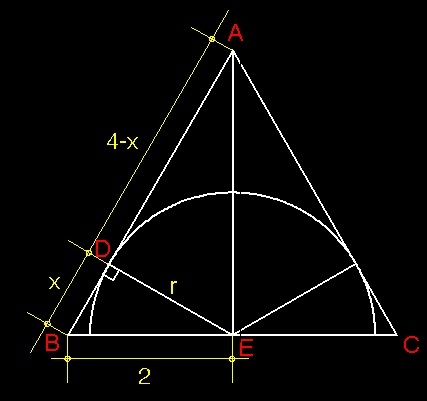
Apply Pythagorean Theorem at right △ B D E ⟹ r 2 = 2 2 − x 2 = 4 − x 2
Apply Pythagorean Theorem at right △ E D A ⟹ r 2 = ( 1 2 ) 2 − ( 4 − x ) 2 = − 4 + 8 x − x 2
r 2 is equal to r 2 ⟹ 4 − x 2 = − 4 + 8 x − x 2 ⟹ 1 = x
Solving for r , we get ⟹ r 2 = 4 − 1 2 = 4 − 1 = 3 ⟹ r = 3 .
Hence, d = 2 r = 2 3 ≈ 3 . 4 6 4
Let r be radius of circle and h the height of triangle. The vertical line would cut the triangle in two equal half triangles with sides 4,2 and h. The area of half triangle with base 2 is 2h/2=h and with base 4 and height r is 4r/2=2r. Therefore, 2r=h. Using Pythagoras theorem, h^2+2^2=4^2, implies h=2√3.Hence, 2r=h=2√3.
how does 2r =h , i dint get it ?
Log in to reply
It helps to visualize a third triangle with one side tangent to the top of the circle, and the opposite vertex in the center of the bottom edge of the large triangle.
Use SOH ⟹ s i n e = h y p o t e n u s e o p p o s i t e s i d e
s i n 6 0 = 2 r
r = 2 s i n 6 0
The diameter therefore is
d = 2 r = 2 ( 2 s i n 6 0 ) = 3 . 4 6 4