Too innocent of an integral

Relevant wiki: Integration Tricks

Let $f(x) = y$ , then $f^{-1}(x) = x$ and we have:

$\begin{aligned} I & = \int_e^{1+e^2} f^{-1}(u) \ du & \small \color{#3D99F6} I \text{ is the shaded region in the figure above.} \\ & = \int_e^{1+e^2} x \ dy & \small \color{#3D99F6} \text{Note that } y = x + e^x - 1, \ \frac {dy}{dx} = 1 + e^x \\ & = \int_1^2 x(1+e^x) \ dx \\ & = \frac {x^2}2 + xe^x - e^x \ \bigg|_1^2 \\ & = \frac 32 + e^2 \\ & = \frac 32 \cdot e^0 + 0 \cdot e^1+ 1\cdot e^2 \end{aligned}$

$\implies \displaystyle \sum_{i=0}^n k_i = \frac 52$ and $n=2$ and $A+B+n = 5+2+2 = \boxed{9}$

Relevant wiki: Integration Tricks

Given that we have a function $f$ that is certainly invertible, but not possible through elementary means, we need to resort a method that will allow us to solve it without directly looking for the inverse.

Let us look at the following picture. 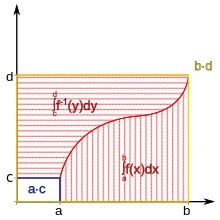This will help us derive a formula for $\displaystyle \int_a^b f^{-1}(x) \mathrm{d}x$ .

$\displaystyle \int_a^b f^{-1}(x) \mathrm{d}x = b f^{-1} (b) - a f^{-1} (a) - \int_{f^{-1}(a)}^{f^{-1}(b)} f(x) \mathrm{d}x$

Now, given that we have $a= e$ , and $b= 1+e^2$ , we just substitute these values on f(x) to be able to find their inverse counterparts.

$e = x + e^x - 1 \:\:\: ; \:\:\: x = f^{-1}(e) = 1$

$1 + e^2 = x + e^x - 1 \:\:\: ; \:\:\: x = f^{-1}(1+e^2)= 2$

Now, we can find the integral.

$\displaystyle \int_e^{1+e^2} f^{-1}(x) \mathrm{d}x = (1+e^2)(2) - (e)(1) - \int_1^2 x + e^x - 1 \mathrm{d}x$

$\displaystyle \int_e^{1+e^2} f^{-1}(x) \mathrm{d}x = (1+e^2)(2) - (e)(1) - \bigg[ \frac{x^2}{2} - x + e^x \bigg]_1^2$

$\displaystyle \int_e^{1+e^2} f^{-1}(x) \mathrm{d}x = 2e^2 - e + 2 - ( e^2 - e + \frac{1}{2} )$

$\displaystyle \int_e^{1+e^2} f^{-1}(x) \mathrm{d}x = e^2 + \frac{3}{2}$

So there, the sum of the coefficients is $\frac{5}{2}$ , and $5+ 2 +2= \boxed{9}$ .

Relevant wiki: Integration Tricks

Note that $f$ is continuous and strictly increasing on its domain; in addition, as $x \to \infty$ , $f(x) \to \infty$ , and as $x \to -\infty$ , $f(x) \to -\infty$ . So $f$ is bijective.

Using substitution $x \gets f(u)$ (valid because $f$ is bijective), we obtain that the bounds become $f^{-1}(e) = 1, f^{-1}(1+e^2) = 2$ (which can be verified by substitution), and the content of the integral, $f^{-1}(x) dx$ , becomes $f^{-1}(f(u)) df(u) = u f'(u) du$ . Since $f'(u) = 1 + e^u$ , the integral becomes

$\displaystyle \int_1^2 u(1+e^u) du$

We can evaluate the integral by parts. Taking $p = u, q' = 1+e^u$ gives $p' = 1, q = u+e^u$ , so

$\displaystyle \begin{aligned} \int u(1+e^u) du &= u(u+e^u) - \int 1(u+e^u) du \\ &= u^2 + ue^u - \frac{1}{2} u^2 - e^u + C \\ &= \frac{1}{2} u^2 + (u-1)e^u + C \end{aligned}$

So we just substitute $u = 1$ and $u = 2$ and take their difference to obtain the value of the integral: $(\frac{1}{2} \cdot 2^2 + (2-1)e^2) - (\frac{1}{2} \cdot 1^2 + (1-1)e^1) = \frac{3}{2} + e^2$ . So $k_0 = \frac{3}{2}, k_1 = 0, k_2 = 1, n = 2$ , giving $A+B+n = 5+2+2 = 9$ .

No solution, just dropped by to say this problem was so much fun!

The inverse function of the limits are trivial (1 and 2 by inspection) so the substitution x=f(u) can be used which gives the integral $\int^{2}_{1} (u+ue^{u})$ Which integrates to $[\frac{u^{2}}{2}+ue^{u}-e^{u}]^{2}_{1}$ this simplifies to $1.5+e^{2}$ so A=5, B=2 and n=2 meaning the answer is 9.