Triangle rotating in triangle, supposedly hard
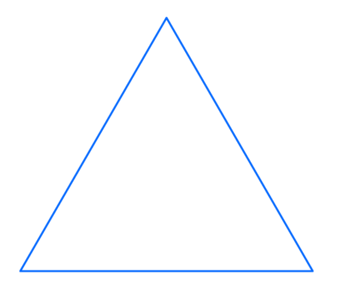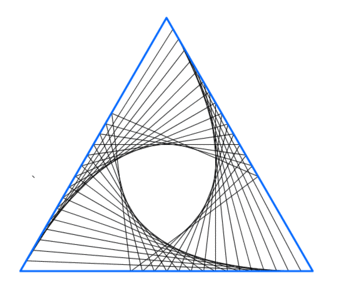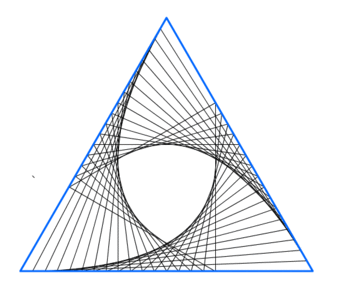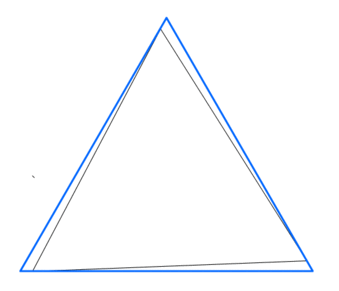
The side lengths of the equilateral triangle (blue in the animation) are 120. Each side gets divided into 24 line segments of lengths 5 cm. The line segments are connected in a way such that a „rotating“ triangle is created.
What is the area of the resulting „shield-like“ figure in the middle of the triangle?
The answer is in the form of . Give the value of k.
The answer is 2000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
In fact, Guy Fox's solution is not a solution of the specified problem at all; but, it is a solution to a closely related problem. The problem statement specifies a Riemann sum of a polygon that is slightly larger than the area enclosed by the caustic curve swept by all the lines that could have swept the interior of the triangle. That problem also would have been a worthy problem. Guy Fox's solution is a worthy answer to that other problem.
Either this problem should be deleted as the answer is wrong or the problem statement should be editted to add a clarification that the Riemann sum is not intended and that the caustic curve result is the correct answer. This clarification must go into the problem statement itself. Adding the clarification in a comment is not sufficient.
Now, a solution to the specified problem. I also have Wolfram Mathematica 11.3.
The lines that actually enclose the polygon. But the corners of the polygon present an additional problem and will be handled separately.
The intersections of the green lines with themselves:
g = Table [ RegionIntersection [ Line [ ( t 1 2 0 − 2 t 0 1 2 0 3 − 3 ( 1 2 0 − 2 t ) ) ] , Line [ ( t + 5 1 2 0 − 2 t + 5 0 1 2 0 3 − 3 ( 1 2 0 − 2 t + 5 ) ) ] ] , { t , 4 0 , 7 5 , 5 } ] ⟹ { Point [ ( 2 1 2 5 2 1 5 3 ) ] , Point [ ( 8 5 3 5 8 7 5 3 ) ] , Point [ ( 8 5 6 5 8 3 2 7 5 ) ] , Point [ ( 4 2 9 5 4 5 5 3 ) ] , Point [ ( 4 3 0 5 4 6 5 3 ) ] , Point [ ( 8 6 2 5 8 3 4 5 5 ) ] , Point [ ( 8 6 3 5 8 1 7 5 3 ) ] , Point [ ( 8 0 2 5 3 ) ] }
The intersections of the blue lines with themselves.
b = Table [ RegionIntersection [ Line [ ( 1 2 0 − 2 t 6 0 − 2 t 1 2 0 3 − 3 ( 1 2 0 − 2 t ) 3 ( 6 0 − 2 t ) ) ] , Line [ ( 1 2 0 − 2 t + 5 6 0 − 2 t + 5 1 2 0 3 − 3 ( 1 2 0 − 2 t + 5 ) 3 ( 6 0 − 2 t + 5 ) ) ] ] , { t , 4 0 , 7 5 , 5 } ]
{ Point [ ( 2 1 5 5 2 5 5 3 ) ] , Point [ ( 2 1 4 5 4 1 1 5 3 ) ] , Point [ ( 2 1 3 5 4 3 3 5 5 ) ] , Point [ ( 2 1 2 5 3 0 3 ) ] , Point [ ( 2 1 1 5 3 0 3 ) ] , Point [ ( 2 1 0 5 4 3 3 5 5 ) ] , Point [ ( 2 9 5 4 1 1 5 3 ) ] , Point [ ( 2 8 5 2 5 5 3 ) ] }
The intersections of the red lines with themselves.
r = Table [ RegionIntersection [ Line [ ( 6 0 − 2 t t 3 ( 6 0 − 2 t ) 0 ) ] , Line [ ( 6 0 − 2 t + 5 t + 5 3 ( 6 0 − 2 t + 5 ) 0 ) ] ] , { t , 4 0 , 7 5 , 5 } ]
{ Point [ ( 4 0 2 5 3 ) ] , Point [ ( 8 3 2 5 8 1 7 5 3 ) ] , Point [ ( 8 3 3 5 8 3 4 5 5 ) ] , Point [ ( 4 1 7 5 4 6 5 3 ) ] , Point [ ( 4 1 8 5 4 5 5 3 ) ] , Point [ ( 8 3 9 5 8 3 2 7 5 ) ] , Point [ ( 8 4 2 5 8 7 5 3 ) ] , Point [ ( 2 1 1 5 2 1 5 3 ) ] }
The three corner points as they involve lines from two different colored line sets.
p1 = RegionIntersection [ Line [ ( t 1 2 0 − 2 t 0 1 2 0 3 − 3 ( 1 2 0 − 2 t ) ) ] /. t → 4 0 , Line [ ( 6 0 − 2 t t 3 ( 6 0 − 2 t ) 0 ) ] /. t → 8 0 ] ⟹ Point [ ( 6 0 3 2 0 ) ]
p2 = RegionIntersection [ Line [ ( 1 2 0 − 2 t 6 0 − 2 t 1 2 0 3 − 3 ( 1 2 0 − 2 t ) 3 ( 6 0 − 2 t ) ) ] /. t → 4 0 , Line [ ( t 1 2 0 − 2 t 0 1 2 0 3 − 3 ( 1 2 0 − 2 t ) ) ] /. t → 8 0 ] ⟹ Point [ ( 8 0 3 8 0 ) ]
p3 = RegionIntersection [ Line [ ( 6 0 − 2 t t 3 ( 6 0 − 2 t ) 0 ) ] /. t → 4 0 , Line [ ( 1 2 0 − 2 t 6 0 − 2 t 1 2 0 3 − 3 ( 1 2 0 − 2 t ) 3 ( 6 0 − 2 t ) ) ] /. t → 8 0 ] ⟹ Point [ ( 4 0 3 8 0 ) ]
Then, assemble the corner points of the polygon: p = Flatten [ { { p1 } , g , { p2 } , b , { p3 } , r } , 1 ] ; .
Then, assemble the polygon: polygon = Polygon [ Flatten [ p /. Point → List , 2 ] ] ; .
Then, get the Riemann sum area (the area of the polygon): area = Evaluate [ Area [ polygon ] ] ⟹ 4 2 6 7 5 3 .
Then, convert to requested form: Solve [ area = 3 u , u ] ⟹ { { u → 4 8 0 2 5 } } .
The answer to the specified problem is 2 0 0 6 . 2 5 .