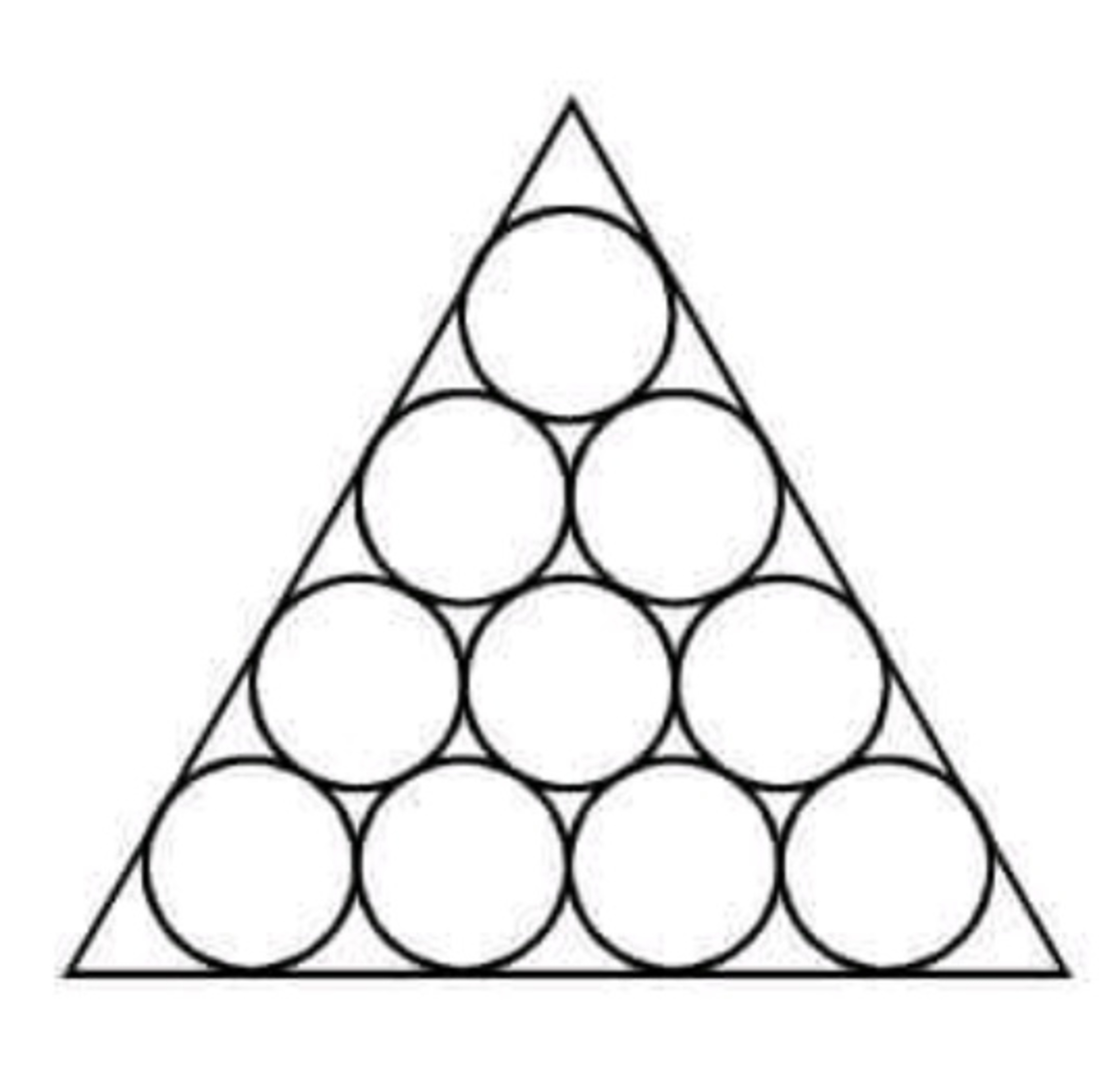
Too many circles in a triangle

Calculus Level 3

Suppose that circles of equal diameter are packed tightly in $n$ rows inside an equlateral triangle such that there are n circles in $n$ th row. If $A$ is the area of the triangle and $A_n$ is the total area occupied by the circles in $n$ rows, find $\displaystyle\lim_{n\to\infty}{A_n}/{A}$ (the diagram shows an example of $n=4$ rows).

\pi\sqrt{3}

\pi/ \sqrt{3}

\pi/6

\pi/ ({2}\sqrt{3})

1 solution

Chew-Seong Cheong
May 13, 2017

Let the radius of the circle be $r$ and the distance between the point where the end circle touches side of the triangle to the vertex of the triangle be $a$ . Then, $a = \dfrac r{\tan 30^\circ} = \sqrt 3 r$ . The side length the triangle with $n$ rows is given by $b = (n-1)(2r) + 2a = 2r(n-1+\sqrt 3)$ . Then, we have:

$\begin{aligned} \lim_{n \to \infty} \frac {A_n}A & = \lim_{n \to \infty} \frac {\frac 12 n(n+1) \pi r^2}{\frac 12 \cdot \frac {\sqrt 3}2b^2} \\ & = \lim_{n \to \infty} \frac {\frac 12 n(n+1) \pi r^2}{\frac {\sqrt 3}4 \cdot 4r^2(n-1+\sqrt 3)^2} \\ & = \boxed{\dfrac \pi {2\sqrt 3}} \end{aligned}$

Too many circles in a triangle

1 solution

0 pending reports