Too Many Sides, Too Little Information
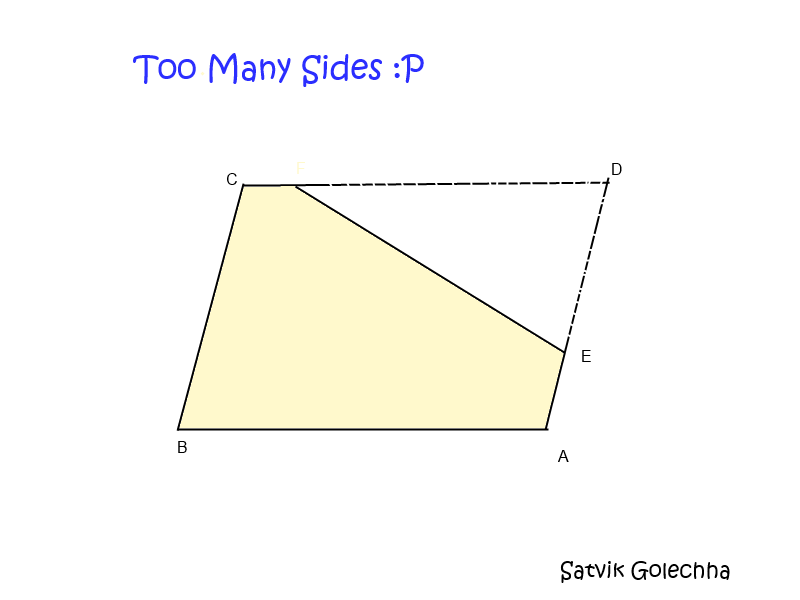 An equiangular quadrilateral ABCD has integral sides. A straight cut is made, which divides it into a triangle with integer sides, and a pentagon with a perimeter of 108 units. Given that four of the sides of the pentagon are 24, 18, 17 and 10 units, what is the area of the triangle (in square units)?
An equiangular quadrilateral ABCD has integral sides. A straight cut is made, which divides it into a triangle with integer sides, and a pentagon with a perimeter of 108 units. Given that four of the sides of the pentagon are 24, 18, 17 and 10 units, what is the area of the triangle (in square units)?
This question was given to me by a teacher.
The answer is 60.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Exactly!! This question can only be solved by ruling out different options......
The key is pythagorean triples "8, 15 , 17"
Thinking that the one who set the question is smart, I didn't assume the triangle to be a right-angle triangle. I used the Heron's formula, where area A = s ( s − a ) ( s − b ) ( s − c ) and s is a half of the perimeter, s = 2 a + b + c to compute the area. I assumed the two of the three longer sides of the pentagon, 1 8 , 2 4 and 3 9 ( = 1 0 8 − 1 7 − 1 8 − 1 0 − 2 4 ) to be the sides of the parallelogram. Then subtract the two sides with a short length to get the two sides of the triangle with the remaining untouched length as the third side. With the help of a spreadsheet and by trial and error, it was found that only when a = 3 9 − 2 4 = 1 5 , b = 1 8 − 1 0 = 8 and c = 1 7 that gave s = 2 1 5 + 8 + 1 7 = 2 0 and area A = 2 0 ( 5 ) ( 1 2 ) ( 3 ) = 6 0 .
@Satvik Golechha , I don't know there may be an integer sided triangle that fits the problem.
Let the position of the cut at CD be F. In the triangle FDE, the sum of the lengths of any two sides must be longer than the remaining side. Call this theorem 1.
We know that the numbers that we can play with is 39, 24, 18, 17 and 10. Two differences must be larger than the remaining number, e.g. 39-14=15, 18-10=8, remaining number 17. 15+8>17, 15+17>8, 17+8>15. By Heron's formula, area of FDE is 60 sq units.
First, ABCD is a rectangle. Next,the 5th side of the pentagon has a length of 39 units. The angled side of the pentagon must be the hypotenuse of a Pythagorean triple. The only possible lengths of the angled side are then 10, 17 and 39 units. We can rule out 39, (since 39^2 is greater than the sum of the squares of any two of the other side lengths), so we are left with 10 and 17 as the possible lengths. With the width of ABCD being 39, the height being 18 and an angled side of length 17, the other two sides of the pentagon have lengths 24 and 10, leaving us with an 8,15,17 right triangle, which has an area of 60.