Too many solutions give me a break!

AB, BC, CD are the sides given. So we want to find the length of the fourth side DA. O is the cercum center, and R its radius = $200\sqrt2.$ As normal we will investigate the half right angled triangles. M is the midpoint of BC, so MOB is such a triangle where $2\phi$ is the angle the side BC makes at the center O.
$\therefore ~\color{#3D99F6}{Sin\phi=\dfrac{100}{200*\sqrt2}=\dfrac 1{2*\sqrt2} }.\\ \implies,\text{Total angle the three sides make at the center is DOA = }6\phi.\\$ $\text{This is also the angle DA makes at the center.} ~~\therefore ~ ~in ~\Delta NOA, ~ \frac 1 2 DA=\color{#3D99F6}{NA=OASin(3\phi)}\\ But ~~Sin(3\phi)= - 4Sin^3\phi + 3 Sin\phi= - \dfrac 1 {4\sqrt2} +\dfrac 3 {2\sqrt2}=\dfrac 5 {4\sqrt 2}\\ \implies ~DA= 2*NA=2*200\sqrt2*Sin(3\phi)= \Large ~~\color{#D61F06}{\boxed { ~~500~~} }\\ ~~\\$

An observation. ABCD is an isosceles trapezium.

Hope my handwriting is legible

Consider $\Delta ABC$ . As we know two of its sides and the circumradius, we can find $AC=100\sqrt{14}$ . Similarly, $BD=100\sqrt{14}$ . Now, using Ptolemy's theorem, $AD=500$ .

Without all these zero's

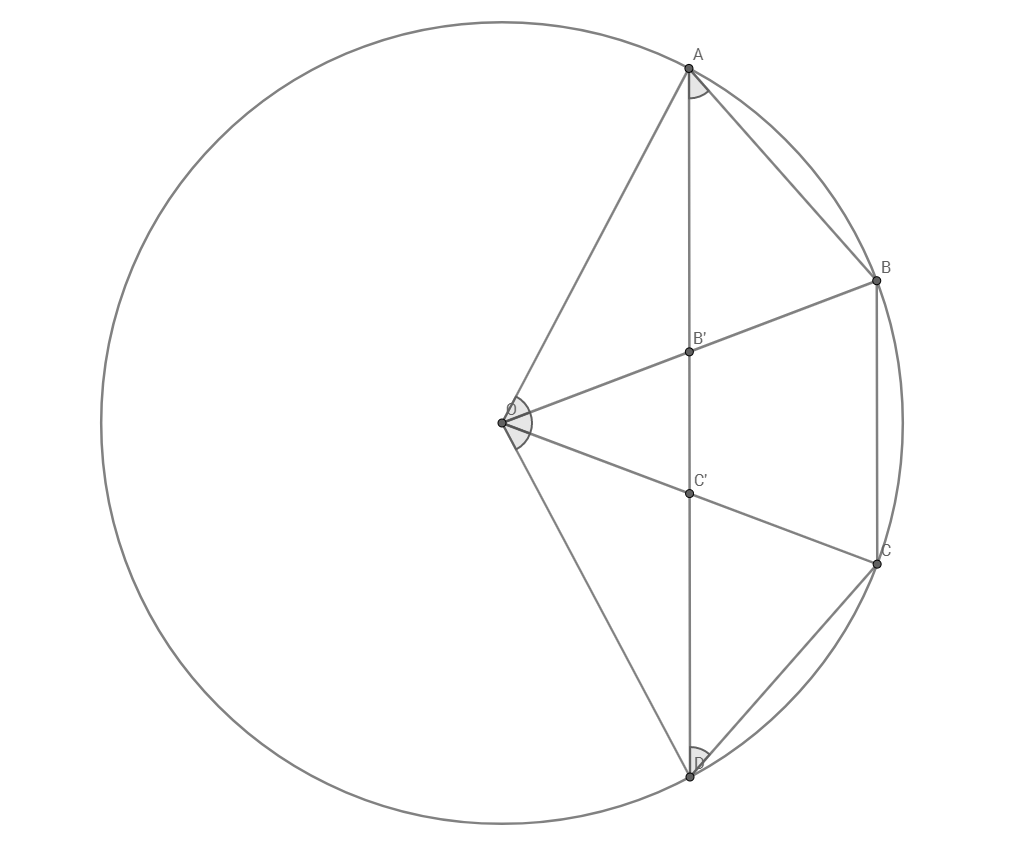
It is very easy to see, from the relation between inscribed and central angles in a circumference, that $\angle A\hat { D } C=\angle C\hat { O } D$ . This means the triangles $\triangle OCD$ and $\triangle DC'C$ are similar. Furthermore, since $\overline{OC}=\overline{OD}$ , both of them are isosceles, which gives us: $\overline { DC' } =\overline { DC }=200$ The similarity also implies that $\frac { \overline { CD } }{ \overline { CC' } } =\frac { \overline { OC } }{ \overline { CD } }$ Substituting what we found, this gives us $\overline { CC' } =100\sqrt { 2 }$ which means $C'$ is the midpoint $\overline{OC}$ This gives us $\overline { B'C' } =\frac { \overline { BC } }{ 2 } =100$ Finally, since $\overline{AB'=DC'}$ (from symmetry), we have $\overline{AD}=\overline{AB'}+\overline{B'C'}+\overline{C'D}=200+100+200=500$