Too Many Triangles?

Probability Level 4

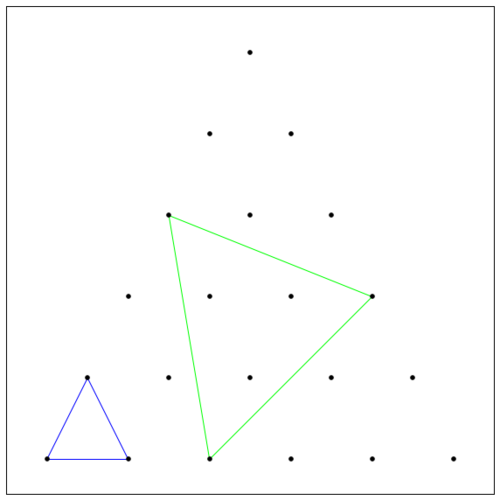How many equilateral triangles can you make by joining the dots with straight lines on this equilateral triangular lattice of perimeter length 6?

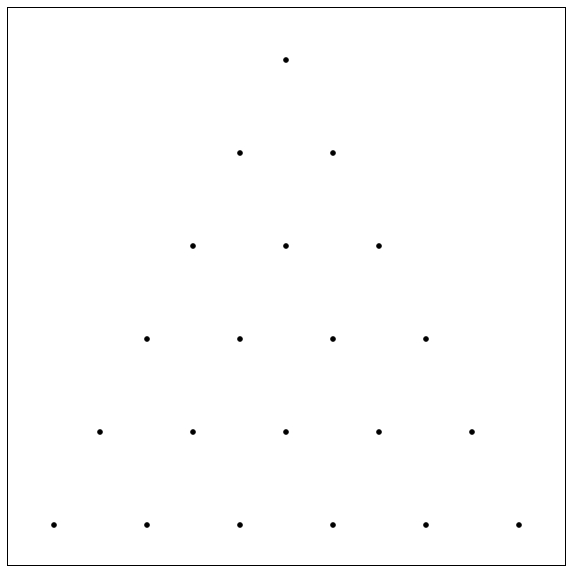
Details and Assumptions :

  • Assume the dots are in a perfect equilateral triangular lattice. My image is slightly stretched.

  • The Two Triangles in the above image are both valid examples of unique Equilateral Triangles.

Inspiration .

Can't get enough of Counting Triangles? Try this question.
120 36 25 70 55

View wiki
Roberto Nicolaides by Roberto Nicolaides , 26, United Kingdom

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

The general formula for n n dots on the outer perimeter is given by ( n + 2 4 ) {n+2 \choose 4} . Since we have 6 dots on the outer perimeter we have a total of ( 8 4 ) = 8 × 7 × 6 × 5 24 = 70 {8 \choose 4} = \frac{8 \times 7 \times 6 \times 5}{24} = 70 unique equilateral triangles we can make.

Proof of the general formula is given here.

Let's count them all!

Let "Count so far" = 0. We'll use this to count them as we go.

  • We can make 15 of these. So now "Count so far" = 15. = 15.

  • We can make 10 of these structures, each containing 2 new triangles we haven't counted before. So "Count so far" = 15 + 10 × 2 = 35 = 15 + 10 \times 2 = 35

  • We can make 6 of these structures each containing 3 new triangles we haven't counted before. So "Count so far" = 35 + 3 × 6 = 53 = 35 + 3 \times 6 = 53

  • We can make 3 of these structures each containing 4 new triangles so "Count so far" = 53 + 3 × 4 = 65. = 53 + 3 \times 4 = 65 .

  • Finally we add the last five triangles we haven't counted before to give "Count so far " = 65 + 5 = 70. = 65 + 5 = 70.

4 Helpful 0 Interesting 0 Brilliant 0 Confused

Alternatively, if we don't insist on finding a closed form solution, we can argue like this: Let f ( n ) f(n) be the number of triangles we can fit into this pattern when there are n n dots along each (outer) edge. (We are asked to find f ( 6 ) f(6) .) Using the inclusion-exclusion principle, we see that f ( n ) f(n) = #(triangles that hit all three edges) + 3(triangles that miss the top right edge) - 3(triangles that miss both top edges) + (triangles that miss all three edges) = ( n − 1 ) + 3 f ( n − 1 ) − 3 f ( n − 2 ) + f ( n − 3 ) (n-1) + 3f(n-1) -3f(n-2) +f(n-3) . Using f ( 0 ) = f ( 1 ) = 0 f(0) = f(1) = 0 and f ( 2 ) = 1 f(2) =1 we find f ( 3 ) = 5 , f ( 4 ) = 15 , f ( 5 ) = 35 f(3) = 5, f(4) = 15, f(5) = 35 and f ( 6 ) = 70 f(6) = 70 .

Otto Bretscher - 6 years, 2 months ago

Nice one!!!!!

Nihar Mahajan - 6 years, 2 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...