Too Tangent
The configuration shows 4 circles of radius 2 and 4 circles of radius 1, all passing through a common point. Find the area of the red regions, where exactly 3 circles overlap.
Note: Each pair of circles are either tangential, or intersect at 90 degrees.
The answer is 3.1275.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
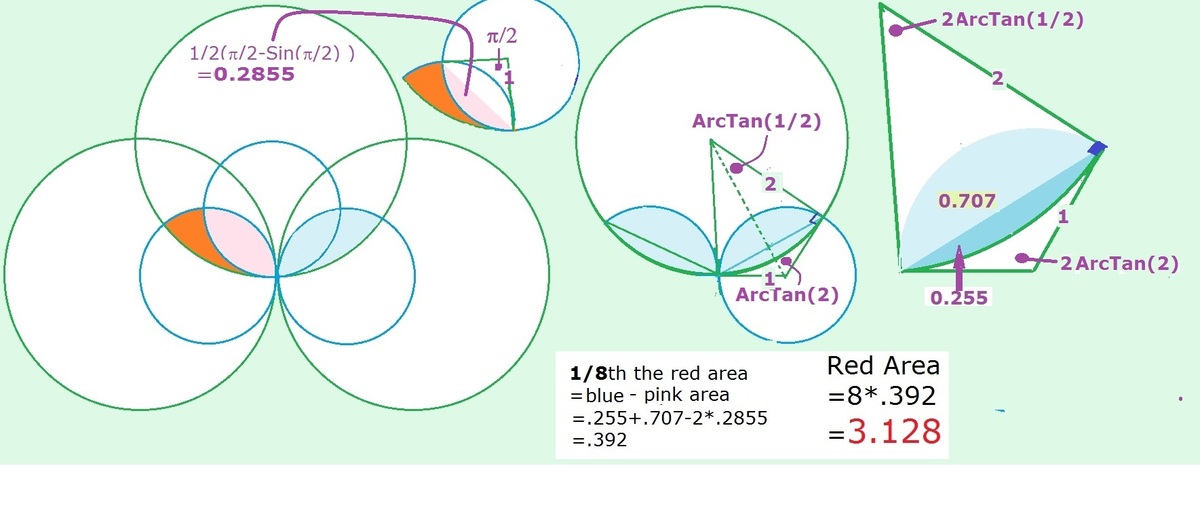
The arrangement is composed of two sets of circles, those going horizontally through the center and those going vertically. Either set may be called the original four circles, with the other set being those intersecting them. The area where three circles overlap is composed of 8 regions such as the one marked in red below.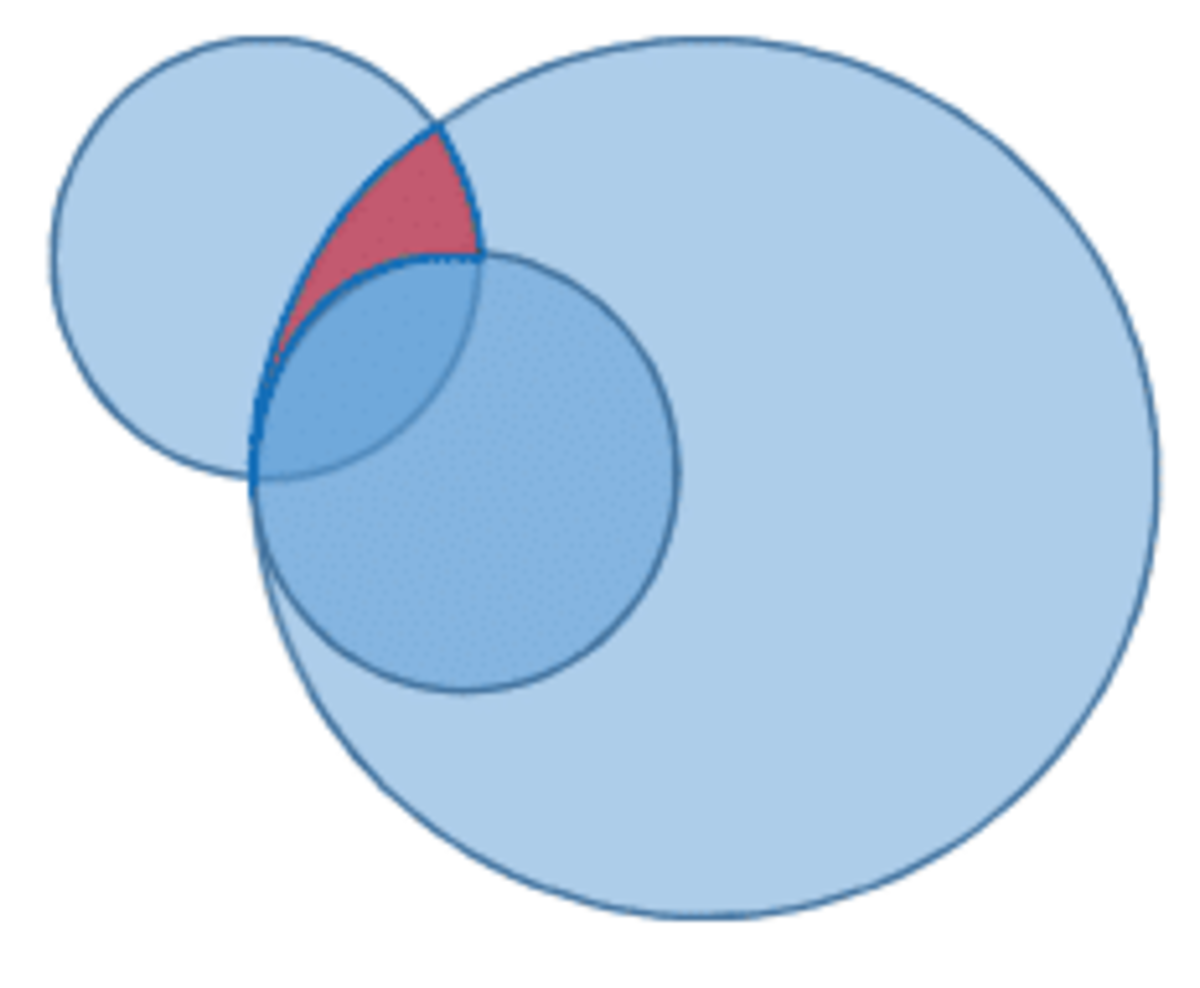
To calculate it, we need the area of overlap of a circle radius 1 with a circle radius 2, intersecting at right angles, and subtract from it area of two circles radius 1 intersecting each other, again at right angles.
To get the first, we can work with circle radius 1 centered at ( 0 , 1 ) and circle radius 2 centered at ( 2 , 0 ) . They will intersect at ( 0 , 0 ) and ( 5 4 , 5 8 ) . This will give us central angle of 1 2 6 . 8 7 ∘ in the smaller circle, 5 3 . 1 3 ∘ in the larger one. The formula for the area of a circular segment with central angle α in degrees is:
A = 2 R 2 ( 1 8 0 α π − s i n ( α ) )
The segment contributed by the smaller circle will have area 0 . 7 0 7 , the other 0 . 2 5 4 6 , giving us a total of 0 . 9 6 1 7 .
The overlapping area of the two small circles will come to 2 π − 1 . Subtracting that and multiplying the result by 8 will give us the final answer, 3 . 1 2 7 5 .