Too Ugly?
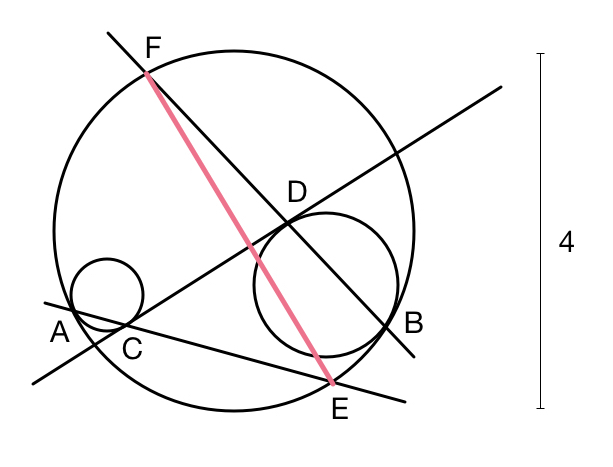
In a large circle of diameter 4, we draw two circles that are each internally tangent at and We then draw the common interior tangent If intersects the large circle at and intersects the large circle at what is the distance
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We will repeatedly use the following lemma in homothety .
Proof: Consider the expansion mapping about point T that brings the smaller circle to the larger circle.
Then, we see that map will bring point A to point B. Also, by considering the tangent to the circle, we see that it will bring the tangent at A to the tangent at B.
Since the expansion mapping keeps the slope of a line constant, this means that the tangent at A will have the same slope as the tangent at B, thus they are parallel. □
Now, on to the original problem.
Construct the tangents at E and F.
Step 1: From the above lemma, the tangent at E is parallel to the tangent at C.
Step 2: From the above lemma, the tangent at F is parallel to the tangent at D.
Step 3: From the previous steps, the tangent at E is parallel to the tangent at F.
Step 4: EF is a diameter of the circle.
Note: As observed by Michael, EF is perpendicular to CD. This follows because the diameter EF is perpendicular to the tangent at E, which is parallel to CD.