Tooth Fairy Problem

Geometry Level 2

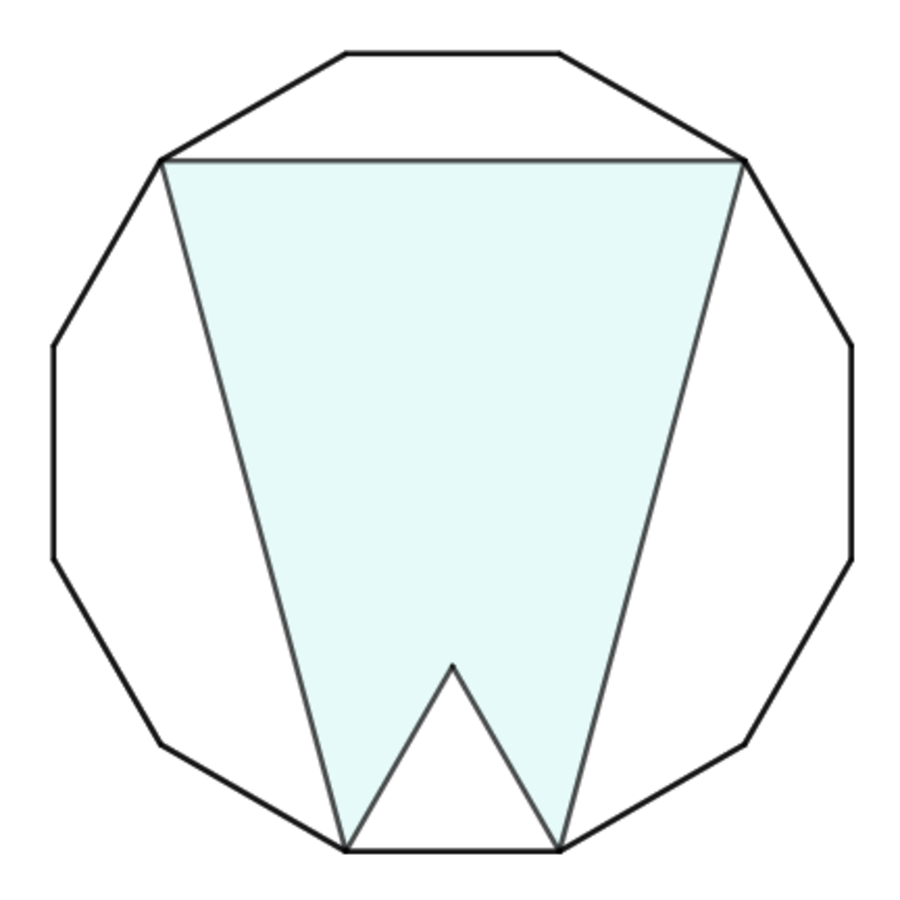
In the regular dodecagon, five segments are drawn to form a blue region, one white equilateral triangle, one white quadrilateral and two white pentagons.

Which of the following, concerning the areas of the $\text{White}$ (inside the dodecagon) and the $\color{#3D99F6}\text{Blue}$ regions, is true?

\text{White}<{\color{#3D99F6}\text{Blue}}

\text{White}={\color{#3D99F6}\text{Blue}}

\text{White}>{\color{#3D99F6}\text{Blue}}

3 solutions

Thanos Petropoulos
Mar 10, 2021

$O$ is the center of the polygon.

This nice partition is a visual “proof without words”.

Felix Belair
Mar 11, 2021

By rule of thumb, the areas will always be the same, since they try to trick you by making one section seem bigger.

Fletcher Mattox
Mar 10, 2021

While I much prefer Thanos' solution, I can't resist a "solution with words", albeit computer words.

# https://www.geogebra.org/classic/ucka3mt2

from sympy import *

# use a dodecagon with circumradius = 1
# it has a total are of 3, which makes the numbers come out nice
p12 = RegularPolygon((0,0), 1, 12, pi/12)
A,B,C,D,E,F,G,H,I,J,L,K = p12.vertices
bi = Line(B, I)
bj = Line(B, J)
ei = Line(E, I)
ej = Line(E, J)
be = Line(B, E)
M = bi.intersection(ej)[0]
p5 = Polygon(I, E, F, G, H).area
p3 = Polygon(I, J, M).area
p4 = Polygon(E, B, C, D).area
white = simplify(p3 + 2*p5 + p4)
print("white=", white)
blue = Polygon(M, J, B, E, I).area
print("blue=", blue)

1 2	`white= 3/2 blue= 3/2`

Tooth Fairy Problem

3 solutions

0 pending reports