Torque on a Dam
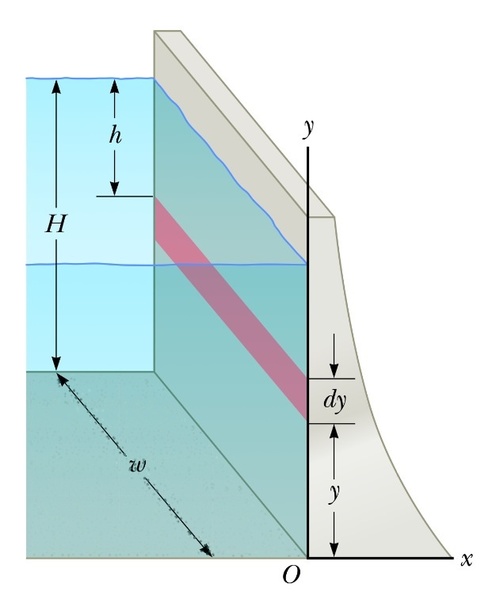 Water exerts a force on the dam. It also exerts a torque about the axis passing through O in the figure. The net force the water exerts on the dam can be modeled to act at a height
above O (So the torque exerted by the water is
). What is
?
Water exerts a force on the dam. It also exerts a torque about the axis passing through O in the figure. The net force the water exerts on the dam can be modeled to act at a height
above O (So the torque exerted by the water is
). What is
?
You can neglect the atmospheric pressure as it acts on both sides of the dam
This Problem is taken from Physics for Scientists and Engineers with Modern Physics
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Force acting on the area w d y is
d F = P d A = P w d y = ρ g ( H − y ) w d y
∫ d F = ∫ 0 H ρ g ( H − y ) w d y
F = 2 1 ρ g w H 2
Next, we calculate the net torque about O.
d τ = y d F = P y d A = ρ g ( H − y ) w y d y
∫ d τ = ∫ 0 H ρ g ( H − y ) w y d y
τ = 6 1 ρ g w H 3
Now we model the net force we calculated earlier on to act at a distance h above O to produce this torque
F h = τ
2 1 ρ g w H 2 h = 6 1 ρ g w H 3
h = 3 1 H ⇒ 1 + 3 = 4