Torus, Monte Carlo, Random Numbers and Volume

Level 2

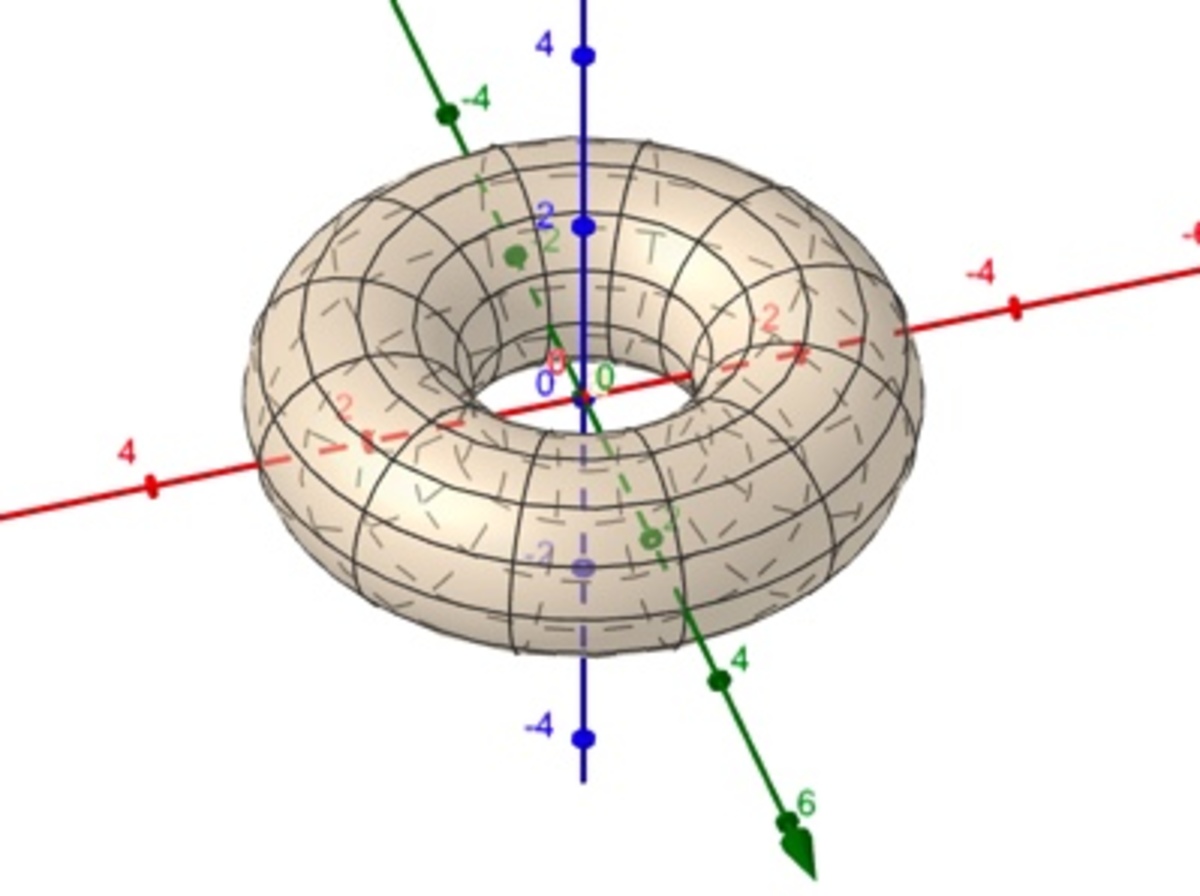Use the Monte Carlo method for finding volume. Calculate the volume of a Torus with the axis of revolution having a radius of 2 and the circle cross section having a radius of 1. All graphs are created using the app. GeoGebra.


The answer is 39.4.

Frank Petiprin by Frank Petiprin , 81, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Piotr Idzik
May 21, 2020

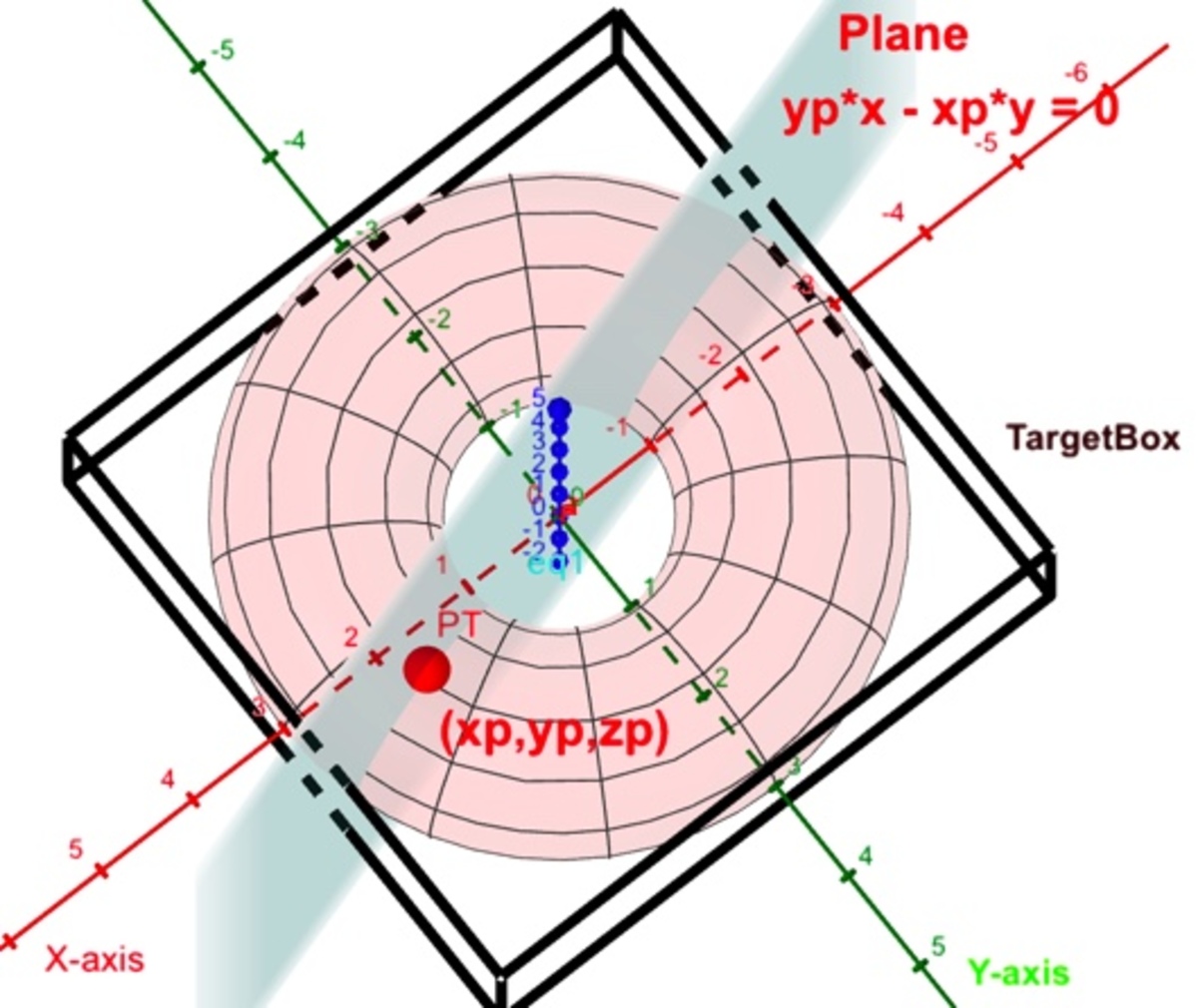
Below you will find my parallel C++ code. Due to the symmetry of the torus, I did the Monte Carlo test only in one of the octants. The result of it is 1 8 \frac{1}{8} of the entire volume. 

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
 
#include <iostream>
#include <cmath>
#include <random>
#include <vector>
#include <chrono>
#include <thread>
#include <ctime>
#include <algorithm>

template<std::size_t Dimension, typename ValueType, typename RandomEngineType, typename IsInsideType>
class McWorker
{
    private:
        const IsInsideType isInside;
        const std::uintmax_t localIter;
        std::array<std::uniform_real_distribution<ValueType>, Dimension> pointGenerator;
        RandomEngineType randomEngine;
        ValueType amountInside;

    public:
        explicit McWorker(const std::array<std::pair<ValueType, ValueType>, Dimension>& _limitBox,
                          const IsInsideType& _isInside,
                          const std::uintmax_t _localIter,
                          const int _seed) :
        isInside(_isInside),
        localIter(_localIter),
        pointGenerator(),
        randomEngine(_seed),
        amountInside()
        {
            for(std::size_t curDim = 0; curDim < Dimension; ++curDim)
            {
                const auto curLimit = _limitBox[curDim];
                this->pointGenerator[curDim] = std::uniform_real_distribution<ValueType>(curLimit.first,
                                                                                         curLimit.second);
            }
        }
        void operator()()
        {
            for(std::uintmax_t curIter = 0; curIter < this->localIter; ++curIter)
            {
                const auto curPos = this->getRandomPoint();
                if(this->isInside(curPos))
                {
                    ++this->amountInside;
                }
            }
        }
        ValueType GetAmountInside() const
        {
            return this->amountInside;
        }
    private:
        std::array<ValueType, Dimension> getRandomPoint()
        {
            std::array<ValueType, Dimension> res;
            for(std::size_t curDim = 0; curDim < Dimension; ++curDim)
            {
                res[curDim] = this->pointGenerator[curDim](this->randomEngine);
            }
            return res;
        }
};

template<typename UnsignedIntType>
UnsignedIntType gcd(const UnsignedIntType _a, UnsignedIntType _b)
{
    UnsignedIntType a, b;
    if(_a > _b)
    {
        a = _a;
        b = _b;
    }
    else
    {
        a = _b;
        b = _a;
    }
    while(b > 0)
    {
        const UnsignedIntType div = a%b;
        a = b;
        b = div;
    }
    return a;
}

template <std::size_t Dimension, typename ValueType>
ValueType getTotalMeasure(const std::array<std::pair<ValueType, ValueType>, Dimension>& limitBox)
{
    auto prodFun = [](const ValueType tmpProd, const std::pair<ValueType, ValueType>& curDim)->ValueType
    {
        return tmpProd*(curDim.second-curDim.first);
    };
    return std::accumulate(limitBox.begin(), limitBox.end(), 1.0L, prodFun);
}

template <std::size_t Dimension, typename ValueType, typename RandomEngineType, typename IsInsideType>
ValueType MeasureMcPar(const std::array<std::pair<ValueType, ValueType>, Dimension>& limitBox,
                       const IsInsideType& isInside,
                       const std::uintmax_t totalIter,
                       const unsigned numberOfThreads)
{
    if(totalIter%std::uintmax_t(numberOfThreads) != 0)
    {
        throw std::invalid_argument("totalIter must be a multiple of numberOfThreads.");
    }
    const std::uintmax_t localIter = totalIter/std::uintmax_t(numberOfThreads);
    std::vector<std::thread> threadVector;
    typedef McWorker<Dimension, ValueType, RandomEngineType, IsInsideType> WorkerType;
    threadVector.reserve(numberOfThreads);
    std::vector<WorkerType> workerVector;
    workerVector.reserve(numberOfThreads);
    const auto mainSeed = time(NULL);
    for(unsigned i = 0; i < numberOfThreads; ++i)
    {
        workerVector.push_back(WorkerType(limitBox, isInside, localIter, i+mainSeed));
        threadVector.push_back(std::thread(std::ref(workerVector[i])));
    }
    for(auto & th : threadVector)
    {
        th.join();
    }

    auto sumFun = [](const std::uintmax_t tmpSum, const WorkerType& inWorker)->std::uintmax_t
    {
        return tmpSum+inWorker.GetAmountInside();
    };
    const std::uintmax_t totalSum = std::accumulate(workerVector.begin(), workerVector.end(), 0ULL, sumFun);
    const auto div = gcd(totalSum, totalIter);
    const auto limitingMeasure = getTotalMeasure<Dimension, ValueType>(limitBox);
    return limitingMeasure*ValueType(totalSum/div)/ValueType(totalIter/div);
}

template <typename ValueType>
class IsInsideTorus
{
    const ValueType rA, rB;
    public:
        IsInsideTorus(const ValueType& _rA, const ValueType& _rB) :
            rA(_rA),
            rB(_rB)
        {}
        bool operator()(std::array<ValueType, 3> inPos) const
        {
            const ValueType x2 = std::pow(inPos[0], 2.0L);
            const ValueType y2 = std::pow(inPos[1], 2.0L);
            const ValueType z2 = std::pow(inPos[2], 2.0L);
            return std::pow(std::sqrt(x2+y2)-this->rA, ValueType(2.0))+z2 <= this->rB*this->rB;
        }
};


int main()
{
    typedef IsInsideTorus<long double> IsInsideType;
    const long double R = 2, r = 1;
    const long double PI = std::atan(1.0L)*4;
    const long double trueVolume = 2*PI*PI*R*r;
    const IsInsideType isInTorus(R, r);
    const std::array<std::pair<long double, long double>, 3> boxTorus = {std::make_pair(0.0L, 3.0L),
                                                                         std::make_pair(0.0L, 3.0L),
                                                                         std::make_pair(0.0L, 1.0L)};

    const unsigned numberOfThreads = std::thread::hardware_concurrency();
    const std::uintmax_t totalIter = std::uintmax_t(numberOfThreads)*50000000ULL;

    const auto startTime = std::chrono::steady_clock::now();
    const auto res = 8*MeasureMcPar<3, long double, std::mt19937_64, IsInsideType>(boxTorus,
                                                                                   isInTorus,
                                                                                   totalIter,
                                                                                   numberOfThreads);
    const auto endTime = std::chrono::steady_clock::now();
    std::chrono::duration<double> runTime = endTime-startTime;
    std::cout<<"Runtime: "<<runTime.count()<<" [s]"<<std::endl;
    std::cout<<"result: "<<res<<" trueValue: "<<trueVolume<<" error: "<<res-trueVolume<<std::endl;
    return 0;
}

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Frank Petiprin
Oct 26, 2019 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
 
The Torus algorithm randomly generates a point PT(xp,yp,zp) in the TargetBox (Volume 72).
Next it finds the equation of a plane PL(yp*x-xp*y=0) (plane is perpendicular to xy-plane
and contains PT(xp,yp,zp)). It then calculates the plane PL intersection PI(xi,yi,0) with
the Torus center circle x**2+y**2=4. Finally it checks the distance  PT(xp,yp,zp ) 
to PI(xi,yi,0). If the distance  is less then or equal to 1 then the point 
PT(xp,yp,zp) is contained in the Torus. (See Diagram) Above

import Numpy as np 
#findHitsInTorus counts the number of times points (xp,yp,zp) are contained in the Torus.     
def findHitsInTorus(xp,yp,zp): #xp yp zp are column arrays 
    xi=2/np.sqrt(1+(yp*yp)/(xp*xp)) #PI:(xi,yi,0) intersects the plane PL and thr Torus’s
    yi=np.sqrt(4-xi*xi)                        # center circle x**2+y**2=4
    TorF=((xi-np.abs(xp))**2+(yi-np.abs(yp))**2+zp**2)<=1 #Distance PT is from PI
    SumTF=sum(TorF)  #sums the Trues in TorF
    return SumTF 
#End findHitsInTorus            
#Main
seed=9001
#np.random.seed(seed) #Use as needed for testing
Trials,Hits,TotVolTorus=10,10000000,0
TarS=3 #Target Side Length
TarH=1 #Target Height
TargetBoxVol=6*6*2
for i in range(1,Trials+1):
    x,y,z=np.random.uniform(-TarS,TarS,Hits),np.random.uniform(-TarS,TarS,Hits)
        z=np.random.uniform(-TarH,TarH,Hits)
    HitsInTor=findHitsInTorus(x,y,z)
    VolTorus=(HitsInTor/Hits)*TargetBoxVol
    print('Total (x,y,z)''s In The TORUS',HitsInTor,'Volume Of Torus',VolTorus,'Trial',i)
    TotVolTorus+=VolTorus
print('Average Volume ',TotVolTorus/Trials)
print('Answer Vol.',4*np.pi**2,'Target Box Vol.',72)
Total (x,y,z)s In The TORUS 5486020 Volume Of Torus 39.4993 Trial 1
Total (x,y,z)s In The TORUS 5482143 Volume Of Torus 39.4714 Trial 2
Total (x,y,z)s In The TORUS 5484161 Volume Of Torus 39.4859 Trial 3
Total (x,y,z)s In The TORUS 5482254 Volume Of Torus 39.4722 Trial 4
Total (x,y,z)s In The TORUS 5483287 Volume Of Torus 39.4796 Trial 5
Total (x,y,z)s In The TORUS 5483943 Volume Of Torus 39.4843 Trial 6
Total (x,y,z)s In The TORUS 5482171 Volume Of Torus 39.47123 Trial 7
Total (x,y,z)s In The TORUS 5480988 Volume Of Torus 39.4631 Trial 8
Total (x,y,z)s In The TORUS 5485935 Volume Of Torus 39.4987 Trial 9
Total (x,y,z)s In The TORUS 5486176 Volume Of Torus 39.5004 Trial 10
Average Volume  39.48269

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...