Tossing coins

Probability Level 4

Suppose a fair coin is tossed $3$ times independently at random. If $X$ is a random variable denoting the number of heads among the $3$ tosses, what is the minimum value of $E \left[ \left| X-a \right| \right]$ for any real number $a$ ?

The answer is 0.75.

2 solutions

Tomas T
Nov 20, 2019

There are 8 possible outcomes for tossing a coin 3 times: {TTT, TTH, THT, THH, HTT, HTH, HHT, HHH}. One of them has no heads, three have one head, three have two heads and finally one has three heads. Therefore, the expected value can be computed as follows:

$E[|X-a|]=\frac{1 \times |0-a| + 3 \times |1-a| + 3 \times |2-a| + 1 \times |3-a|}{8}$

If we draw the above fraction as a graph: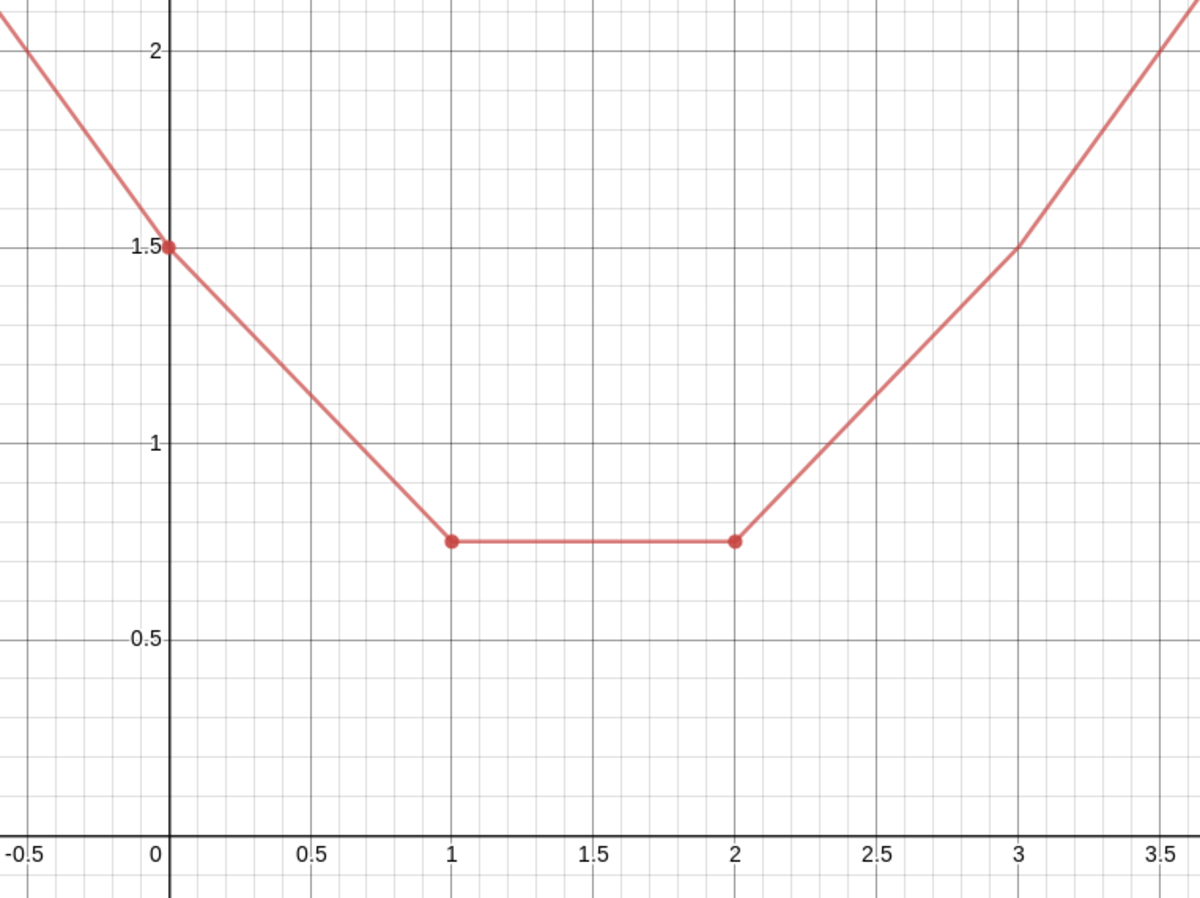

We can see that $y$ takes the lowest value, namely $y=0.75$ when $x \in [1;2]$ .

Ajinkya Shivashankar
Nov 3, 2016

The minimum value will occur at a=1.5, thus |X-a| can be 0.5 or 1.5. using probabilities we can say that expected value is 0.75

For a more general solution calculate E[|X-a|] for a belongs to: i)negative, ii)0 to 1 iii)1 to 2 iv)2 to 3 v) 3 to infinite

You could now say that 2 cases can be avoided as function is symmetrical about x=1.5 as the actual probabilities are symmetrical about 1.5. you could further reduce it to only 1 case by another trick.(try finding it). then finally solving for extrema using very basic calculus.

Ajinkya Shivashankar - 4 years, 7 months ago

Tossing coins

The answer is 0.75.

2 solutions

0 pending reports