Total acceleration (Class XII Maharashtra board problem)
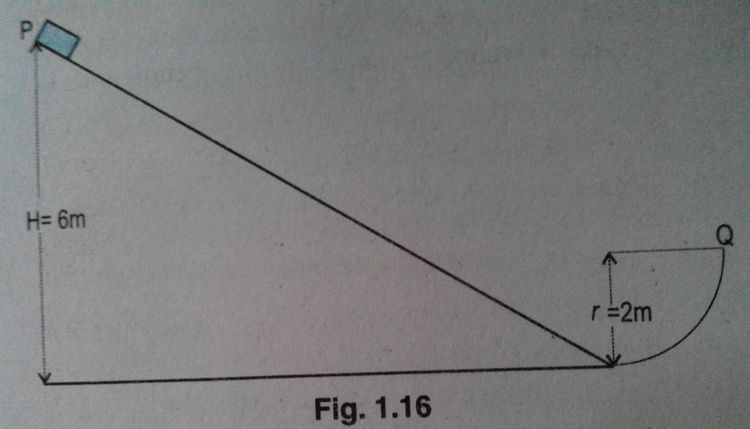A block of mass 1kg is released from P on a frictionless track which ends in quarter circular track of radius 2m at the bottom. What is the magnitude of total acceleration when it reaches at point Q? (g=9.8m/s)
The answer is 40.41.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Discussions for this problem are now closed
But considering the motion in the circular portion as motion in vertical circle, the tangential acceleration is g s i n θ . At Q the angle θ = 9 0 ∘ . Thus, a t = g
Thanks dude for clarifying it
there are two components of a at q one toward center of circular path and other is tangential to path and a(tang) is a= -g (as Zidane Elyousfi has said ) where g is its magnitude 9.81 and -ve sign is showing that body is decelerating ( moving against gravity and it will stop at a point). so direction of a(tang) is opposite to the motion of body (when body decelerates then direction of a is opposite to the motion of body) , as body at Q move to up so direction of a(tang) is downward. I hope your difficulty has removed, if not then ask Mr. Zidane Elyousfi
How can tangential acceleration be equal to 'g' it aint a free fall
Since the surface is frictionless, the tangential acceleration will be same as accelaration due to gravity.
sorry sorry m wrong
here tangential acceleration is in upward direction not downward. it is the pseudo one !!!
Pankaj... in this case total acceleration has two components, one equal to 'g' in downward direction and one in the direction from point Q to the center of the curved path equal to V^2/2... here V is the velocity at point Q and it can be calculated from the energy conservation law......Rahul Tudu you are not right because when a body moves in a circular path, its acceleration is towards the center of curvature of the path.....
I think that a=gsin(theta) from point P to the base. Then, a=g*(sin(arc tangent of the curve)) and sin(arc tangent of the curve))=-1 at Q.So at Q a = -9.8.what you guys think
please , I didn't understand why the acceleration at Q is g .. according to the second law of Newton we will have -mg=ma which gives a=-g so a=-9.8m/s² not a=9.8m/s² .. please can anyone clarify me this ?
ya you are right the tangential acceleration is − g at Q but in the upward direction.But i only took the direction of the acceleration in downward direction(+ve). But along its direction of motion(upward direction) it is decelerating(g is -ve). By the way @Shahbaz Amjad has a good explanation.
first the tangential acceleration a(t) equal to g=9.8m/s^2. which is in down ward direction. The second acceleration is centripetal aceleration a=v^2/r
but can the tangential acceleration not be the right answer? it is also the acceleration at point Q.
Yes, it is easy to forget that one has to add the downward component of acceleration. One could also find the above b looking at the kinetic energy at the bottom equating it to loss of potential energy and then go on to subtract the gain in potential energy equal to the radius which would then give the value of kinetic energy at Q and hence the value of the centripetal acceleration
I think this answer is wrong, if you people look at it theoretically, it is impossible, if this block have an acceleration of 40.41 m/sec^2 soon it will achieve escape velocity, which is impossible, in my opinion the answer should be -g.
i think the question is incomplete. neither is the base or the hypotenuse given nor is it stated anywhere that the triangle is an isosceles so one can't actually know how fast the box is going to come at the bottom of the triangle
Well I found and interesting way to solve this The initial potential energy P=MgH And final energy is E=MgR+1/2(M v^2) Since initially it was at rest the total energy is equal to potential energy selecting ground as the datum So now we have Mgh=MgR+1/2(M v^2) Putting value and solving
We get 1/2(M v^2)=4Mg So Now as it is in a circular motion it has an acceleration of1/2(M v^2) towards the center and this is perpendicular to g So net acceleration is a=√((1/2(M*v^2))^2+g^2) Further a=√((4mg)^2+g^2) Solving and putting the values given u have a=40.4 ms^-2
Answer depends if the object is reaching the point q or leaving the point q...
Dude its at q it doesn't depends
Use Conservation Of mechanical energy With datum at P Find out acceleration at P and then corelate with angular accelation alpha(@)... at point P you will get accelaration 39.2 m/s^2 now... For PQ use law of mechanical consevation of energy... and fing out alpha(@) =3.992 .... Now since we know... accelatration^2=v^+2@^2 therefore frm above soln accelartion total =√(39.2^2+(2×3.992)^2) = 40.41 m/s^2
Thanks dude!
please , I didn't understand why the acceleration at Q is g .. according to the second law of Newton we will have -mg=ma which gives a=-g so a=-9.8m/s² not a=9.8m/s² .. please can anyone clarify me this ?
zidane it depends on the coordinate axes chosen according to your convenience chose upward direction as positive then downward is negative or chose downward direction as positive then upward is negative then accordingly u should modify ur equation as -mg=-ma so that a=g
I basically did what Tejas Kasetty did.
Acceleration[total] = sqrt( Acceleration[Tangential]^2 + Acceleration[Centripetal]^2 )
Acceleration[Tangential] = 9.81m/s^2 due to the surface being frictionless
** The tangential acceleration being equal to g was just an assumption I made, but does that actually make sense? Isn't there a normal force still associated with the object which cancels out a component of the force due to gravity downwards?
Acceleration[Centripetal] = v^2 / r
v = sqrt(2g*d)
v= sqrt(2 9.81 4)
** Come to think of it though, i don't know why I used 4 metres instead of 6 metres.
Firstly by conservation of energy we get velocity at point Q as 8.85. then normal acceleration is v 2 /r which equals to 39.161 .And acceleration due to gravity g acting downward.Taking resultant of these two we get acceleration at point Q as 40.37.
Using conservation of energy , we have m g h = m g r + 2 1 m v 2 . Plugging the values we have r v 2 = 4 g . So centripetal accelaration = 4 g . And also gravitational accelaration g is acting hence total acc. = 1 7 g .
At required pt, u already have an acceleration of g downwards. Conserving energy at initial pt and required pt, u get 6mg=2mg+(1/2)(mv^2)..... Hence, v^2=8g..... At required pt, u hav centripetal acceleration of v^2/r = v^2/2 towards d left..... Using parallelogram law of vector addition, u get net acceleration of g*sqroot(17) which is approximately 40.40!!!
Firstly the tangential acceleration at point Q is a t = g = 9 . 8 m / s 2 , which is acting downwards.
Second one is the centripetal acceleration a c = r v Q 2 ....... (1)
Finding the velocity at Q . By conservation of energy,
m g h = 2 1 m v Q 2 + m g r
Clearly, v Q 2 = 2 g ( h − r ) . Substituting for v Q 2 in (1) we get a c = r 2 g ( h − r ) = 4 g which is along the centre of the arc from Q .
Thus, a n e t = a c 2 + a t 2 = ( 4 g ) 2 + g 2 = g 1 7 = 4 0 . 4 0 6 ≈ 4 0 . 4 1