This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
x + 2 x + 1 + x + 9 x + 8 = x + 3 x + 2 + x + 8 x + 7
⇒ x + 2 x + 2 − 1 + x + 9 x + 9 − 1 = x + 3 x + 3 − 1 + x + 8 x + 8 − 1
⇒ ( 1 − x + 2 1 ) + ( 1 − x + 9 1 ) = ( 1 − x + 3 1 ) + ( 1 − x + 8 1 )
⇒ x + 2 1 + x + 9 1 = x + 3 1 + x + 8 1
⇒ x + 2 1 − x + 3 1 = x + 8 1 − x + 9 1
⇒ x 2 + 5 x + 6 x + 3 − x − 2 = x 2 + 1 7 x + 7 2 x + 9 − x − 8
⇒ x 2 + 5 x + 6 = x 2 + 1 7 x + 7 2 ⇒ 1 2 x = − 6 6 ⇒ x = 5 . 5
How did you get from the original form to the 2nd one?
Log in to reply
Sorry, I have missed a step. I have added it in. See the solution now. Thanks.
Sujoy Roy's method is the best. However, the method below may help in other problems. Hence I give them.
X
+
9
X
+
8
−
X
+
8
X
+
7
=
X
+
3
X
+
2
−
X
+
2
X
+
1
∴
(
X
+
9
)
(
X
+
8
)
(
X
+
8
)
2
−
(
X
+
9
)
(
X
+
7
)
=
(
X
+
9
)
(
X
+
8
)
(
X
+
2
)
2
−
(
X
+
3
)
(
X
+
1
)
⟹
X
2
+
1
7
X
+
7
2
)
1
=
X
2
+
5
X
+
6
1
E
q
u
a
t
i
n
g
t
h
e
r
e
c
i
p
r
o
c
a
l
s
a
n
d
s
i
m
p
l
i
f
y
i
n
g
,
w
e
g
e
t
X
=
−
5
.
5
O
R
X
+
2
X
+
1
+
X
+
9
X
+
8
=
X
+
3
X
+
2
+
X
+
8
X
+
7
∴
X
2
+
1
1
X
+
1
8
X
2
+
1
0
X
+
9
+
X
2
+
1
0
X
+
1
6
=
X
2
+
1
1
X
+
2
4
X
2
+
1
0
X
+
1
6
+
X
2
+
1
0
X
+
2
1
⟹
X
2
+
1
1
X
+
1
8
2
(
X
2
+
1
0
X
+
2
2
5
)
=
X
2
+
1
1
X
+
2
4
2
(
X
2
+
1
0
X
+
2
3
7
)
⟹
2
(
X
2
+
1
0
X
+
2
3
7
)
2
(
X
2
+
1
0
X
+
2
2
5
)
=
X
2
+
1
1
X
+
2
4
X
2
+
1
1
X
+
1
8
⟹
1
−
X
2
+
1
0
X
+
2
3
7
2
1
2
=
1
−
X
2
+
1
1
X
+
2
4
6
E
q
u
a
t
i
n
g
t
h
e
r
e
c
i
p
r
o
c
a
l
s
a
n
d
s
i
m
p
l
i
f
y
i
n
g
,
w
e
g
e
t
X
=
−
5
.
5
The equation can be put in the form
1 - 1/( x + 2 ) + 1 - 1/( x + 9) = 1 - 1/( x + 3 ) + 1 - 1/( x + 8 )
1/( x + 2 ) + 1/( x + 9) = 1/( x + 3 ) + 1/( x + 8 )
( 2 x + 11 )/( x + 2 )( x + 9 ) = (2 x + 11 )/( x+ 3 )( x + 8 )
Since ( x + 2 )( x + 9 ) not equal ( x+ 3 )( x + 8 )
Then
2 x + 11 = 0
x = - 5.5
1-1/(x+2)+1-1/(x+9) = 1-1/(x+3)+1-1/(x+8),
1/(x+2)+1/(x+9) = 1/(x+3)+1/(x+8),
(2x+11)/(x^2+11x+18) = (2x+11)/(x^2+11x+24),
(2x+11)[(x^2+11x+24)-(x^2+11x+18)] = 0,
x = -11/2.
Let x+5 = a a-4/a-3 + a+3/a+4 = a-3/a-2 + a+2/a+3 (a^2 - 16 + a^2 -9) / (a-3)(a+4) = (a^2 - 9 + a^2 -4) / (a-2)(a+3) ( 2 * a^2 - 25 ) / (a-3)(a+4) = ( 2 * a^2 - 13) / (a-2)(a+3) after cross multiplication and expansion of brackets , ( 2 * a^2 - 13 -12) / ( 2 * a^2 - 13) = a^2 + a - 12 / a^2 + a - 6 1 - [12 / ( 2 * a^2 - 13)] = 1 - [6 / a^2 + a - 6] -12 / ( 2 * a^2 - 13) = - 6 / a^2 + a - 6 -12 / ( 2 * a^2 - 13) = -12 / 2( a^2 + a - 6) 2 * a^2 - 13 = 2( a^2 + a - 6) 2 * a^2 - 13 = 2*a^2 + 2a - 12 -13 = 2a -12 a = -1/2 = 0.5 x = -5+a x = -5 - 0.5 = -5.5
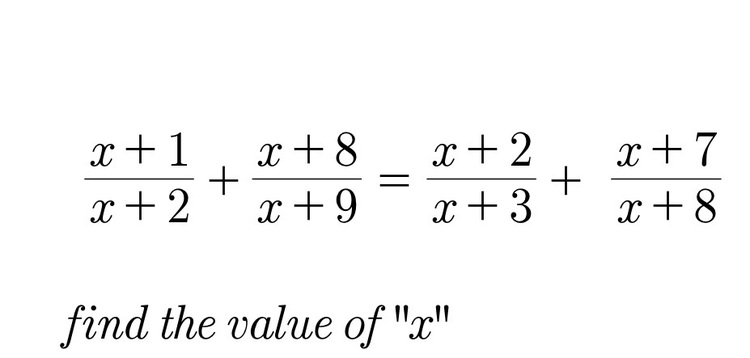
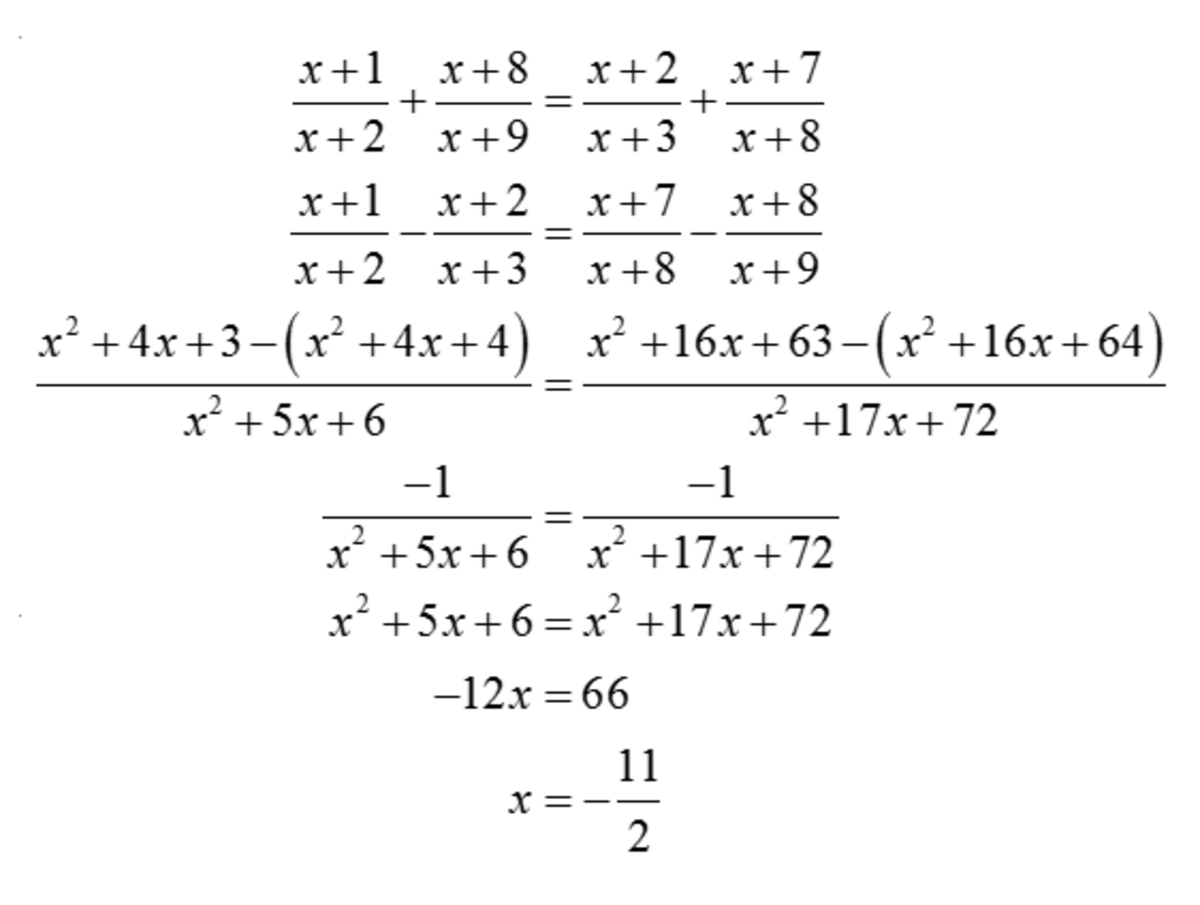
x + 2 x + 1 + x + 9 x + 8 = x + 3 x + 2 + x + 8 x + 7
or, 1 − x + 2 x + 1 + 1 − x + 9 x + 8 = 1 − x + 3 x + 2 + 1 − x + 8 x + 7
or, x + 2 1 + x + 9 1 = x + 3 1 + x + 8 1
or, x + 2 1 − x + 3 1 = x + 8 1 − x + 9 1
or, ( x + 2 ) ( x + 3 ) 1 = ( x + 8 ) ( x + 9 ) 1
or, x 2 + 5 x + 6 = x 2 + 1 7 x + 7 2
or, 1 2 x = − 6 6 or, x = − 5 . 5