Tower of Hanoi

Logic Level 2

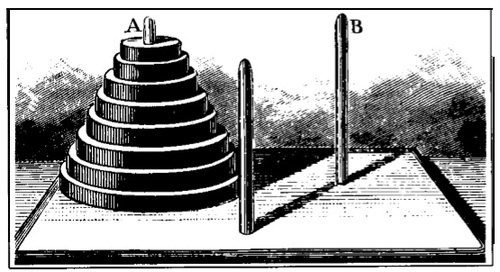
A neat little puzzle called the Tower of Hanoi , invented by the French mathematician Edouard Lucas in 1883.

We are given a tower of 8 disks, initially stacked in decreasing size on 1 of 3 pegs.

The objective is to transfer the entire tower to one of the other pegs, moving only 1 disk at a time and never moving a larger one onto a smaller.

What is the minimum number of moves are required to achieve this goal?

Note : Moving one disk from one peg to another is considered as 1 move.

The answer is 255.

3 solutions

Brandon Monsen
Dec 7, 2015

Let $f(n)$ denote the number of moves needed to move a tower of size $n$ . In order to move a tower of size $n$ , we first need to move a tower of size $n-1$ , move the base of the tower, and then move the tower of size $n-1$ back onto the base. This gives us the recursive formula

$f(n)=2f(n-1)+1$

It is evident that $f(1)=1$ , and so we can arrive at the conclusion that $f(8)=255$

It is quite easy to prove that:

We have $f(1)=2^1-1$ .

Suppose $f(n)=2^n-1$ , we got $f(n+1)=2f(n)+1 = 2(2^n-1)+1 = 2^{n+1}-1$

Tran Hieu - 5 years, 6 months ago

Did you observe that $f(n)=2^n-1$ ?

Akshat Sharda - 5 years, 6 months ago

Yes I did, but I didn't prove it so I left it out of my solution :P

Brandon Monsen - 5 years, 6 months ago

Mohit Gupta
Dec 7, 2015

I had taken two cases first i did it with 3 discs and then with 4 discs...(though it ate my lot of time :p ) however i deduced the soln. To be of the form 2^n -1. Since result i got were 7 and 15 resp. So ans. Is $2^{8}$ -1

By the way is this generalisation true for all integers????

Mohit Gupta - 5 years, 6 months ago

Yes, it is true for all positive integers $n$ .

Akshat Sharda - 5 years, 6 months ago

Siva Prasad
Jan 20, 2016

If n is the number of disks, then no of moves = $2^{n}-1$

Tower of Hanoi

The answer is 255.

3 solutions

0 pending reports