Trace It - 1
Can you trace this
entire
figure:
1) without picking up your writing/tracing tool and
2) without ever doubling back along a line already traced?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
As the puzzle is worded, you can actually trace it with one continuous line. Slightly different wording (... "and not crossing a previously drawn line") turns the problem into a non solvable one (due to the Euler path constraints). So I disagree with the provided answer based on the way the problem is worded.
Log in to reply
I agree with this. No doubling back is necessary to draw or trace this figure and therefore gives a solution as long as intersections are allowed.
Log in to reply
In that figure there are 4 nodes with an odd number of edges (two on the square, and two on the circle). At any node you can either start, stop, cross-over or any combination of those. Since you we are constrained to not double back (and with the exception of where you start and stop for now) each time you enter a node you have to exit - which means those nodes must have an even number of connections. The nodes where you start and stop can have an odd number of edges.
Since you have more than 2 odd numbered nodes you can't trace that figure; as you can't start in more than one place or stop in more than one place.
True, if that was the wording, then it would be possible. However, if you look at the wording: "Can you trace this entire figure: 1) without picking up your writing/tracing tool and 2) without ever doubling back along a line already traced?" You see that it is written that you cannot cross a previously drawn line ("without ever doubling back along a line already traced").
The solution is possible if you don't need to end at the starting point, which not stated as a requirement.
Log in to reply
In that figure there are 4 nodes with an odd number of edges (two on the square, and two on the circle). At any node you can either start, stop, cross-over or any combination of those. Since you we are constrained to not double back (and with the exception of where you start and stop for now) each time you enter a node you have to exit - which means those nodes must have an even number of connections. The nodes where you start and stop can have an odd number of edges.
Since you have more than 2 odd numbered nodes you can't trace that figure; as you can't start in more than one place or stop in more than one place.
It's actually impossible for a graph to have one odd vertex; the total degree of every graph is even because if one vertex has an odd degree, then that edge that makes that vertex odd must connect to another even vertex, thereby making that vertex odd as well. Graphs need to have an even number of odd degree vertices.
Log in to reply
Unless one of the edges has no end vertex... Which is probably nonsensical.
Log in to reply
An edge has to have an end vertex, because by definition, an edge connects two vertices.
Yup, I'll edit the solution. Thanks!
We could always use 2 pencils. It is not stated there that you should use only 1.
Log in to reply
"without picking up your writing/tracing tool" Tool, not tools.
I know the eulerian/semi-eulerian problem but i see this graph as semi eulerian with two nodes of odd degree therefore starting at one odd node you should end at the other?(with the limitations set)
Log in to reply
there are 4 nodes with a odd degree - two on the left and right of the square with degree 3, and two on the left & right of the circle with degree 5.
I traced all the lines without ever doubling back along any line, I did cross a line, but not double back along it. It says I am wrong?????
Log in to reply
Maths says that you are wrong. Think about what happens when you hit a join. If it has an even number of lines you can go in on one line and exit on another and cross that point however many pairs you have. If you have Join (vertex) with an odd number of lines you can’t use every line without doubling back unless you either start or end there. Since you can only start in one place and end in one place that means you can only traverse such a diagram if there is only 2 vortexes with odd line count.
In the diagram given there are 4 which means you can’t move around it and cover every line without doubling back.
I was able to trace the graph with one line without lifting the pencil and without doubling back on any line, so why is it wrong?
Log in to reply
Maths says that you are wrong. Think about what happens when you hit a join. If it has an even number of lines you can go in on one line and exit on another and cross that point however many pairs you have. If you have Join (vertex) with an odd number of lines you can’t use every line without doubling back unless you either start or end there. Since you can only start in one place and end in one place that means you can only traverse such a diagram if there is only 2 vortexes with odd line count.
In the diagram given there are 4 which means you can’t move around it and cover every line without doubling back.
There is an Euler path for 1 odd vertex.
Umm, I just traced it... does the square on the very outside count?
So do I, I literally can trace with one single line and I actually don't understand how it can harm the requirements.
Log in to reply
Maths says that you are wrong. Think about what happens when you hit a join. If it has an even number of lines you can go in on one line and exit on another and cross that point however many pairs you have. If you have Join (vertex) with an odd number of lines you can’t use every line without doubling back unless you either start or end there. Since you can only start in one place and end in one place that means you can only traverse such a diagram if there is only 2 vortexes with odd line count.
In the diagram given there are 4 which means you can’t move around it and cover every line without doubling back.
Great solution and welcome back! Haven't seen you on Brilliant in awhile, Nicole. I smell a path tracing wiki brewing. ;)
I can fold the paper, move my utensil onto the folded flap, and then move it back onto the figure where I need to. It's possible to fulfill all requirements by doing that.
I see only two odd vertices, why the answer is impossible????
Log in to reply
the vertices at the left and right edge of the squares are both odd - 3 connections each, and the vertices at the left and right of the circle are odd - 5 connections each.
Rules also doesn't mention that I can't leave the path to draw an additional path which completes the conditions as stated.
Log in to reply
If you leave the path you aren't tracing the figure any more.
I beg somebody to either give a more detailed solution or give a source/wiki where I can understand this better please... thanks in advance!!
Log in to reply
https://en.wikipedia.org/wiki/Eulerian_path
In summary - imagine any given node - that node can either have an odd or an even number of edges leading from it. We have the rule that we must not double back - so each time we visit a node (excluding where we start or end) we must come to the node along one edge, and go away from the node from another edge - i.e. 'consuming' 2 edges at each visit to a node.
For a node with 2n edges - we must visit it n times to travel along each vertex. For a node with 2n+1 edges we can go through it at most n times and still be able to pass through it, although we still have an edge we have not travelled on to that node (i.e. the +1) - if we travel on that edge it means we must either : 1. Stop at that node (since we have used all the edges from that node). 2. Start at that node - knowing we will go through that node without stopping another n times.
So we have the clear statement that if we have any odd nodes we can only have exactly 2 - one where we start and one where we stop, for the whole path to be traversable without doubling back or without jumping (i.e. lifting pen/finger off the paper). We can have any number of even numbered nodes; and if there are no odd nodes, we can start on any even numbered node and be able to draw a completed path.
The network above has 4 odd nodes : 2 at either side of the square (both with 3 edges from it). 2 at either side of the circle (both with 5 from edges leading from it).
So there are 4 places where you must either start or stop - which as shown above is impossible you can't do if you follow the rules as given.
I traced it in one continuous movement but I did cross over a line (not retraced it). so the puzzle is solvable as stated!!!!
Log in to reply
retracing means following the same line again in either direction. As defined it is impossible to trace the figure as given without re-tracing a line - this is explained clearly a number of times; crossing a line at any given point is entirely valid, but irrelevant. The puzzle as stated is impossible whether you cross lines or not. If you think you traced it correctly that you made a mistake -
The reasoning is as follows :
For the figure as drawn there are exactly 4 points within the figure where there are an odd number of lines emanating from those points - two on the verticals of the squares which each have 3 lines emanating from those points, and one each on either side of the circles which have 5 lines emanating from those points.
Statement 1 : For any figure - when you only start or only stop on a single point you 'consume' one line emanating from a point; when you both enter and exit a point (transit/cross) you consume two lines that emanate from that point.
Conclusion 1: For any figure - for any odd numbered point - it must therefore be either a start or a stop point. It cannot only be a crossing/transit point, since crossings/transit consume 2 lines (as above - statement 1), and it is impossible to make an odd number by summing 2s. It can also not be both a start and stop point (since that consumes two lines).
Conclusion 2 : For any figure with no odd numbered points, you could start anywhere, so long as you stopped there too - since that start and stop will consume a pair of lines into that point.
Conclusion 3: For any figure with only one odd numbered point, you could either start at that odd numbered point but you would have no end point; or stop at that odd numbered point, but have nowhere to start.
Conclusion 4: from Conclusions 1-3 - for a figure to be traceable it must either have exactly zero or exactly two odd numbered points - it cannot have 4 as the figure above does.
In Summary : The given figure has 4 odd numbered points, but since we have been tasked with tracing the line without lifting the pencil (and therefore we can only have one start and one end point); we can therefore state clearly it is impossible to trace all lines in that that figure - regardless of which odd numbered points you start from and which other odd numbered points you stop on, there will be another pair of odd numbered points where it will be impossible for you to have consumed all of the lines from that point. If you start on an even numbered point you can't consume all of the lines in and out of all points (since from above you have to stop and start on an odd numbered points where they exist).
There are seven nodes: two with three branches, three with four branches, and two with five branches. For all paths through a three-branch node to be used, it must be crossed once, and either stopped or started on. Similarly, four-branch nodes need to be crossed twice and five-branch nodes need to be crossed twice, and either stopped or started on.
Since a single path has exactly two endpoints, there are too many odd-branched nodes to start or stop on all of them with just one line. Two will suffice.
great explanation
Both a triangle and circle can only be traced such that the exit point is the same as the initial entry point. Therefore they can be removed from the diagram. Obviously the remaining rectangle and two short legs cannot be traced.
A rectangle can be traced to, by choosing a given start/end node - so by your theory that can also be removed -. I don't think you can reduce the graph like that and still be left always with a set of lines that prove the statement. The only thing that matters is how many even and odd vertices there are - i.e. how many vertices there are that have an even number of lines, and how many there are that have an odd number of lines. See my comments above as to why you can have any number of even vertices, and either zero or two odd vertices. The graph in the question has 4 odd vertices, and therefore can't be traced.
This Graph has two line segments stemming out of the inner circle that connect it to the outer square. Consider the two nodes of intersection between the inner shape and these two lines. If you entered through one, you have to leave at the other since you cannot double back along any line. They both have even number of edges connected to them. WLOG, if entered at the left line segment, then you have to leave at the right one with all the edges of the inner shape covered by your pencil. This mean that the first covered edge connected to the right node is covered from left to right; hence, to cover the next following connected edge to the right node, you have to cover it from right to left. So to cover even number of edges entering from left to right, you have to leave in the opposite direction from right to left which contradicts the fact that we got to leave from the right node. Therefore, such a path doesn't exist.
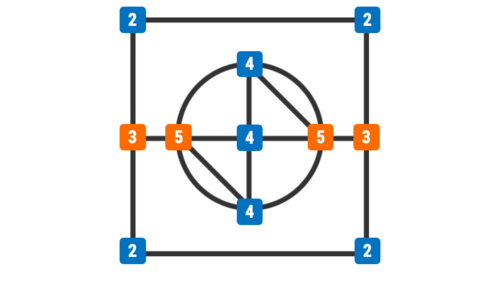The entire figure into a graph with degrees of each node
To be able to trace an Eulerian path, it should have at least two or no odd-degree nodes.
In this figure there are 4 odd-degree nodes, hence it is impossible
I tried by possible way but it’s impossible
It's impossible because if you trace the square you can't trace the figure in the center and the lines on the sides since tracing the two lines doesn't allow you to trace the figure in the center completely and tracing the figure in the center completely doesn't allow you to trace the two lines.
There are two vertices of odd degree.
Nope. There are four.
Log in to reply
My point was: there is more than one vertex of odd degree.
There has to be odd number of options in the circle.. There is even number, so it goes outwards then inwards, outwards then inwards to original position which you are not allowed to overlap lines
For a network to have an Euler path (ie you can trace it fully without repeating a line or lifting your pen), it cannot have more than two odd vertices. (An odd vertex is a vertex with an odd number of connected edges) This figure has more than two odd vertices, and so tracing it given the conditions is impossible.
Food for Thought
This is linked to a famous math question - the Seven Bridges of Könisberg. Euler came up with three theorems when he solved it. In short:
0 odd vertices - at least one Euler circuit (ie the Euler path leads back to the same point you started from)
2 odd vertices - at least 1 Euler path, no Euler circuit
more than 2 - no Euler path
Odd number of odd vertices - no such graph