Tracing a perfect circle

Geometry Level 3

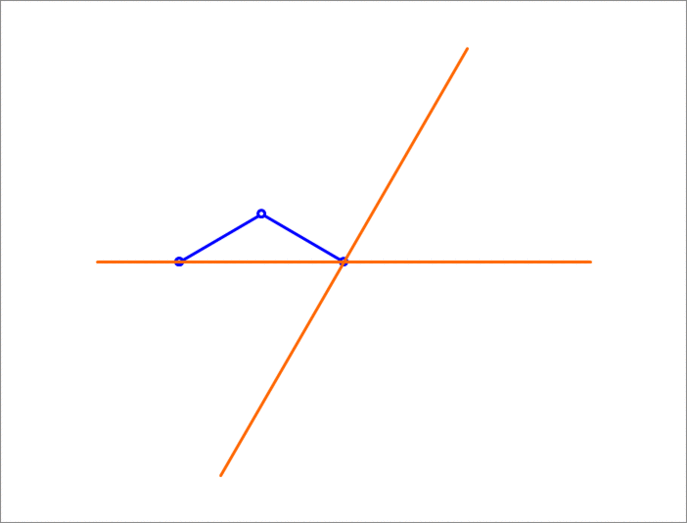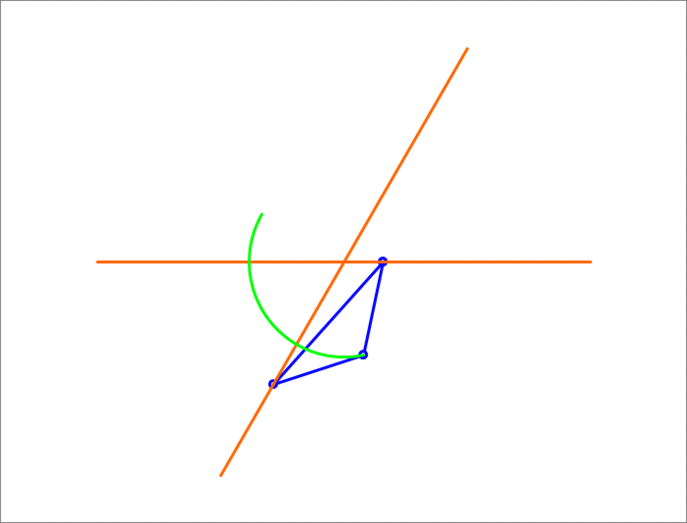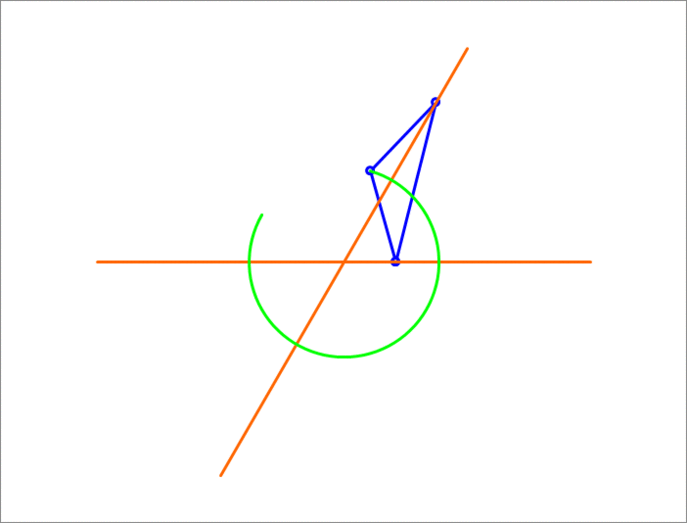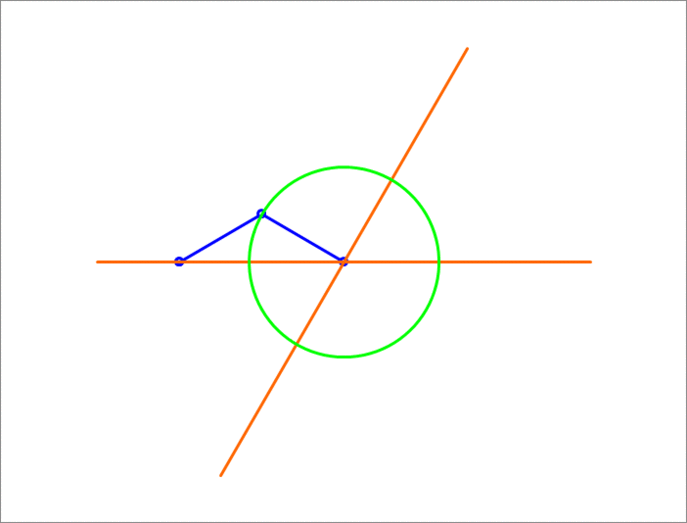
A isosceles triangle has a unit length base sliding on two lines (orange) that make an angle of $60^{\circ}$ between them. The third vertex traces a circle (green). What is the altitude of the triangle?

\dfrac{1}{ \sqrt{3}}

\dfrac{1}{2 \sqrt{3}}

\dfrac{\sqrt{3}}{4}

\dfrac{1}{2}

1 solution

David Vreken
Feb 4, 2019

Let $a$ be the altitude of the isosceles triangle and $r$ be the radius of the circle.

When the unit base of the isosceles triangle is flat against one of the orange lines, the leg is the radius. By Pythagorean's Theorem, $a^2 + (\frac{1}{2})^2 = r^2$ .

When the unit base of the isosceles triangle makes an equilateral triangle with the two orange lines, the radius of the circle and the altitude of the isosceles triangle make up the altitude of a unit equilateral triangle, so $r + a = \frac{\sqrt{3}}{2}$ .

Solving these two equations gives $a = \boxed{\frac{1}{2\sqrt{3}}}$ .

Tracing a perfect circle

1 solution

0 pending reports