Tracing a straight line
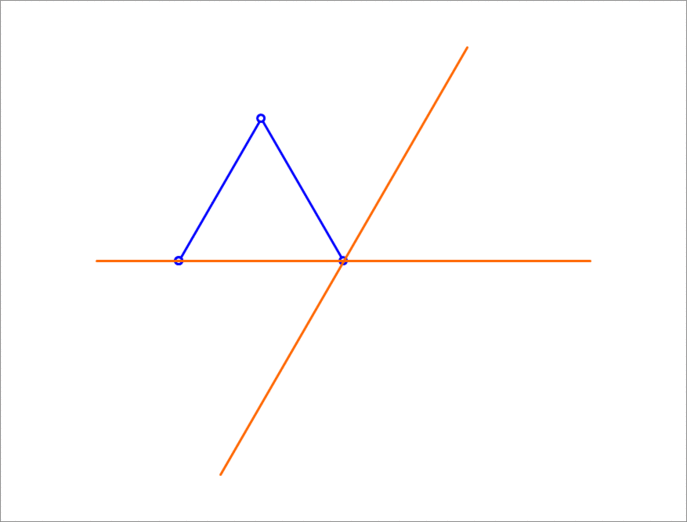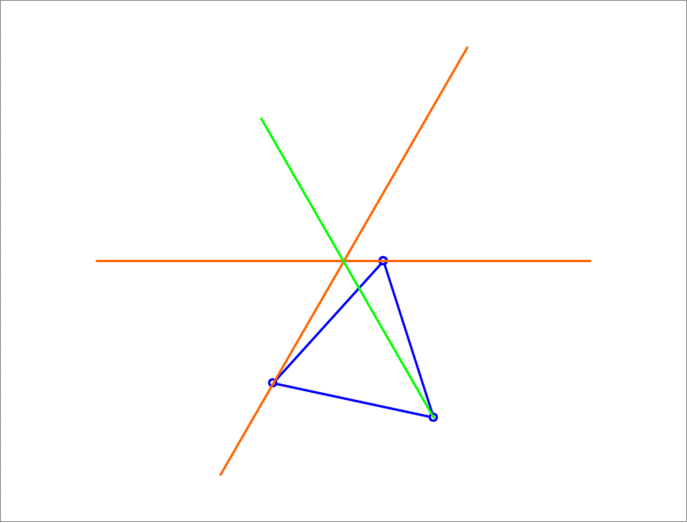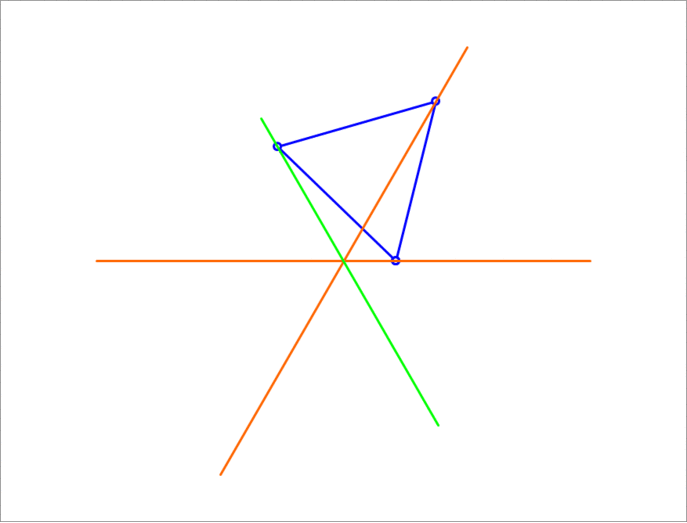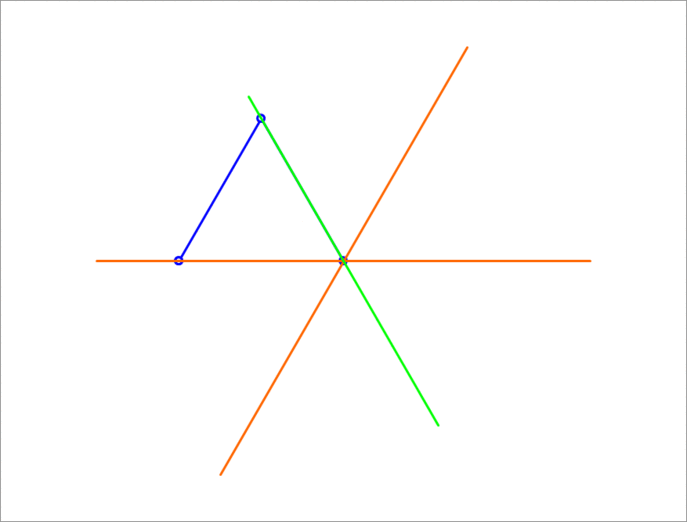
A unit equilateral triangle has two of its vertices sliding on two lines that make an angle of between them. The third vertex traces a straight line segment. Find its length.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
By symmetry, the maximum distance from center of the two intersecting lines O occurs when the two sliding vertices A and B of the equilateral triangle are equal distances away from O , so when A O = B O .
This means △ A O B is an isosceles triangle, and since ∠ A O B = 1 8 0 ° − 6 0 ° = 1 2 0 ° , ∠ O A B = 2 1 8 0 ° − 1 2 0 ° = 3 0 ° and ∠ A O C = 2 1 1 2 0 ° = 6 0 ° . Also, since △ A B C is a unit equilateral triangle, A B = 1 and ∠ B A C = 6 0 ° . This means ∠ O A C = 3 0 ° + 6 0 ° = 9 0 ° .
Solving △ A C O with A B = 1 , ∠ O A C = 9 0 ° , and ∠ A O C = 6 0 ° gives O C = 3 2 . By symmetry the straight line is twice this length, which is 2 ⋅ 3 2 = 3 4 .