Tracing Electric Field Lines
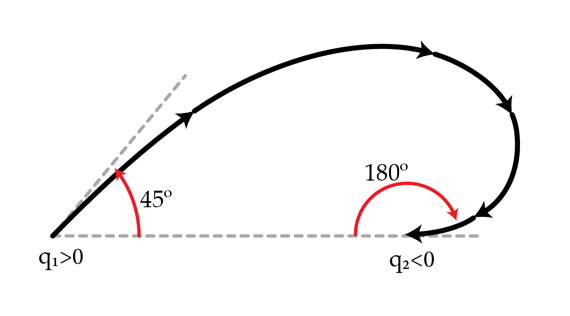 Consider two charges
q
1
>
0
and
q
2
<
0
. An electric field line exits the positive charge
q
1
at
4
5
degrees and enters the negative charge
q
2
at
1
8
0
degrees. What is the ratio
∣
q
2
∣
∣
q
1
∣
?
Consider two charges
q
1
>
0
and
q
2
<
0
. An electric field line exits the positive charge
q
1
at
4
5
degrees and enters the negative charge
q
2
at
1
8
0
degrees. What is the ratio
∣
q
2
∣
∣
q
1
∣
?
The answer is 6.83.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Discussions for this problem are now closed
very nice solution
Instead of considering just one line, let us consider a numerous amount of Field lines that emerge from q 1 and enter q 2 at the respective angles α and β (thus creating a cone in the vicinity of each charge)
Now,
It is a proven fact, and also an obvious one, that the
magnitude
of the charges are
inversely
proportional to the respective
Solid angles
.
We know,
Solid angle
=
2
π
(
1
−
cos
θ
)
, where
θ
is the
half angle
of the cone.
Hence,
∣
q
1
∣
∝
2
π
(
1
−
cos
α
)
1
and
∣
q
2
∣
∝
2
π
(
1
−
cos
β
)
1
Dividing the two equations,
∣ q 2 ∣ ∣ q 1 ∣ = 1 − cos α 1 − cos β = 1 − c o s 4 π 1 − cos π = 1 − 2 1 2 ≈ 6 . 8 3
you can also use more straightfoward geometry to arrive at the solution.
Surface area of a sphere = 4πR^2
Given 45 degrees, the area of the spherical cap 'consuming' the lesser charge: = 2πRh = 2πR^2(1-2^(-1/2))
The ratio of these areas is the ratio of the charges. You could also use volume and a 'spherical sector.'
Where did you find the formula? Please share the link or the name of the book.
Check Wikipedia Here
solve S S Krotov
Yeah, I have solved it..Its the first problem of Krotov..
Standard bookwork tells us that the equation of a general field line is q 1 cos θ 1 + q 2 cos θ 2 = c for some constant c , where θ 1 is the angle that the line from the particle to the charge q 1 makes with the line joining the two charges, and θ 2 is the angle that the line from the particle to the charge q 2 makes with the same line.
When the field line leaves q 1 we have θ 1 = 4 5 ∘ and θ 2 = 1 8 0 ∘ , When the field line enters q 2 we have θ 1 = θ 2 = 0 ∘ . Thus q 1 + q 2 = c 2 q 1 − q 2 = c and solving these simultaneous equations gives ∣ ∣ ∣ q 2 q 1 ∣ ∣ ∣ = 2 − 1 2 2 = 2 ( 2 + 2 ) = 6 . 8 2 8