Track & Trace

Consider the parametric coordinates for the end points of the rod as :

$\displaystyle (t_1,t_1^2)$ $\displaystyle \text{and}$ $\displaystyle (t_2,t_2^2)$

The constraints on these two points is that, the distance between them is always $\displaystyle 4$ .

Thus,

$\sqrt{(t_2^2-t_1^2)^2+(t_2-t_1)^2} = 4$

$\left(t_1^2+t_2^2-2t_1t_2\right)\left(1+t_1^2+t_2^2+2t_1t_2\right) = 16 --- (1)$

This will be our constraint. Now, consider the mid-point of the bar, which has the coordinates :

$\left(X,Y\right) = \left(\frac{t_1+t_2}{2},\frac{t_1^2+t_2^2}{2}\right)$

We need to find the locus of this point.

$X = \frac{t_1+t_2}{2}$ $Y = \frac{t_1^2+t_2^2}{2}$

$\Rightarrow 2X = t_1+t_2 --- (2)$ $\Rightarrow 2Y = t_1^2+t_2^2 --- (3)$

Playing with the above two equations, we get,

$2X^2-Y = t_1t_2 --- (4)$

We can now eliminate $\displaystyle t_1$ and $\displaystyle t_2$ from our constraint equation, by substituting from $\displaystyle (2),(3)$ and $\displaystyle (4)$

Doing so, the constraint equation simplifies to :

$\left(4Y-4X^2\right)\left(1+4X^2\right) = 16$

$Y = X^2 + \frac{4}{1+4X^2}$

We can now switch back to lower-case letters. (I used uppercase to avoid any confusion)

$y = x^2 + \frac{4}{1+4x^2}$

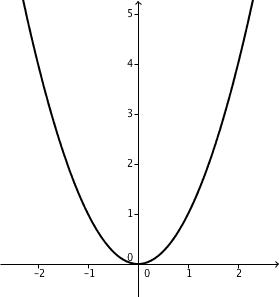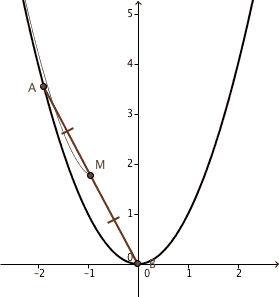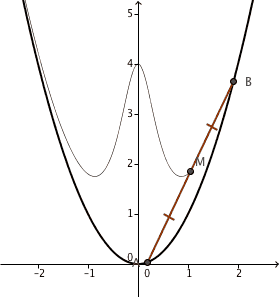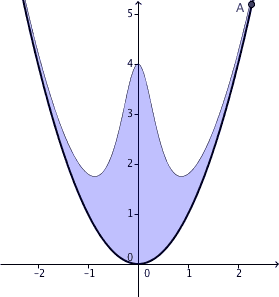
This is the locus of the midpoint of the bar

Now, the area between a function $\displaystyle f(x)$ and $\displaystyle g(x)$ with $\displaystyle f(x)>g(x)$ , is given by the integral of the difference of the functions, with limits as the x-coordinates of the intersection points of the two functions.

Hence, the area between the graph of $\displaystyle y = x^2+\frac{4}{1+4x^2}$ and $\displaystyle y = x^2$ is :

$A = \int_{-\infty}^{\infty} (x^2+\frac{4}{1+4x^2}) - (x^2) dx$

$A = \int_{-\infty}^{\infty} \frac{4}{1+4x^2} dx$

$\boxed{A = 2\pi \approx 6.28}$

Use Holditch's Theorem for this one, imagine a "closed curve" of 2 parabolas joined at infinity. Then the area of the region between this "closed curve" and the locus of the midpoint is 4π. But this problem asks for the area of the region defined by one of the parabolas, so the area is 2π.