Tractor
A tractor moving forward at uniform speed on a horizontal ground has a front wheel diameter of and back wheel diameter of . The horizontal distance between the axles of the two wheels is . During a trip a pebble stuck to the front wheel flew off the wheel at the highest point. 0.2 second later, another pebble flew off the back wheel at its highest point too. The two pebbles landed on the same spot on the ground. Find the speed of the tractor in .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
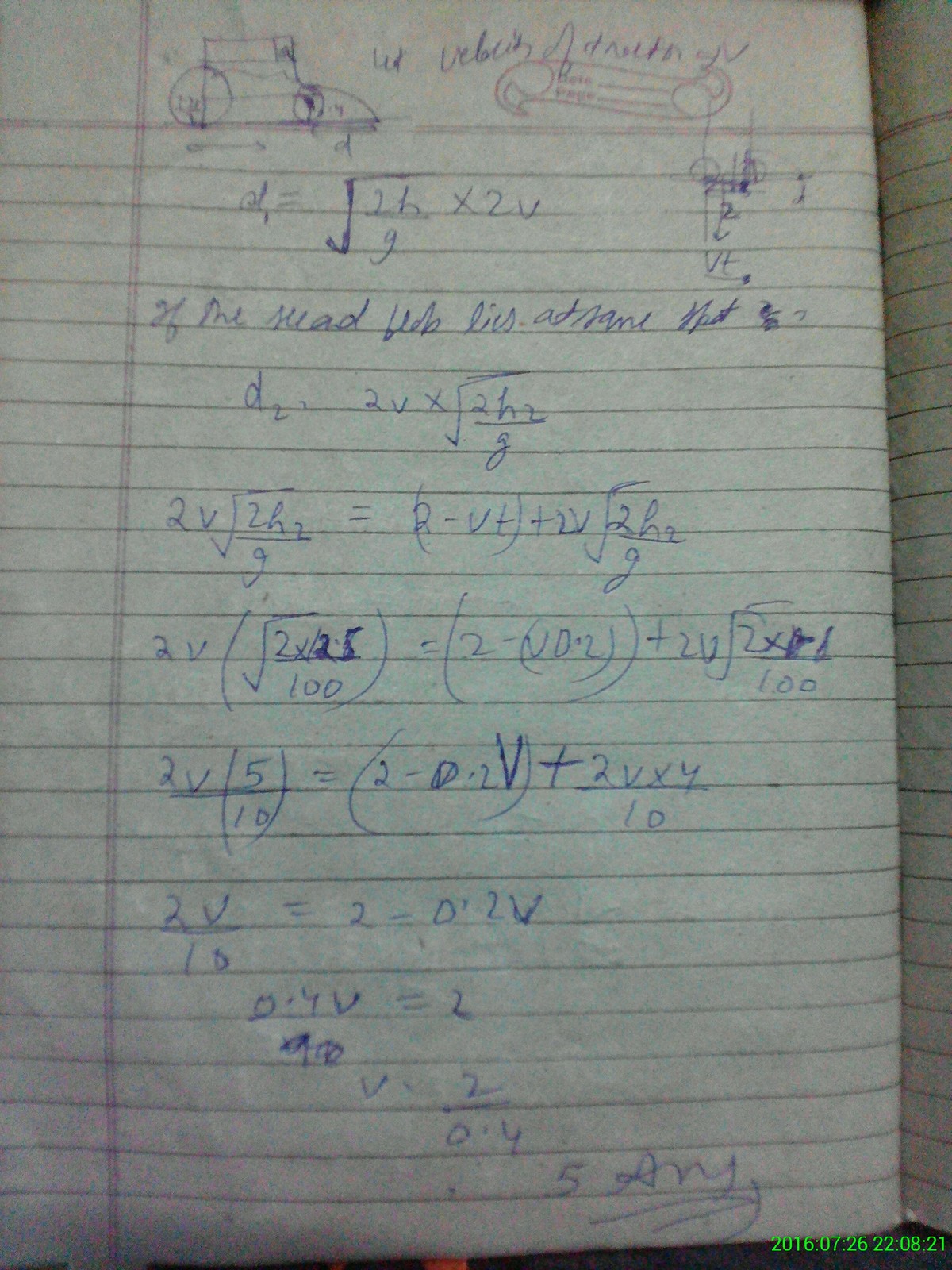
1)Take the 2 wheels as rotating 2d discs. 2)Let the tractor move with speed Vm/s. 3)The two discs have identical velocities of center of masses. 4)Catch: The resultant velocity of the topmost point of a smoothly rotating translatory disc is 2Vm/s. Explanation: please refer any standard book on rotational dynamics. 5)let the first particle travel distance Xm. 6)the time the particle takes to trave this distance is X/(2V). 7) Time taken by particle to reach the ground would be same. I.e. 1/2g(t^2)=0.8 and t=X/(2V). 8)similarly form an equation for the larger wheel keeping in mind the distance of 2m and the consequence of tractor travelling 0.2s at Vm/s. 9)solve these to get V=5m/s. NOTE: TAKE g=10m/s^2 PS: not good at explaining.