Tracy's Triangle Trouble
Like any other boy or girl her age, Tracy enjoys playing with triangles.
However, Tracy has a pretty unique methodology:
- First, she designates a point as 1. This point is "fixed" as far as she is concerned.
- The other two points move within constraints, with point 2 moving units upward and point 3 moving units left (where is any real number and her concept of verticality and horizontality is completely static and will never change).
- If she can flip the triangle twice, she must negate the area between the flips; otherwise, flips don't affect the area. (She doesn't work with triangles that start with 0 area before the pedants among you ask.)
She has discovered, plotting triangle area vs. that she can either find exactly one global maximum xor exactly one global minimum. She has decided to devote all of her time to ensuring that all triangles can fulfill their destiny of having the area of their global maximum or minimum.
The devious villain Jardine, however, likes his triangles just the way they are. Being a student of human nature, he can predict with 100% accuracy which points on his triangles she will designate as 1, 2, and 3.
Can Jardine get Tracy to leave any arbitrary triangle alone by simply rotating it?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
So, a triangle is just half of a parallelogram. I'm going to follow through with an arbitrary example.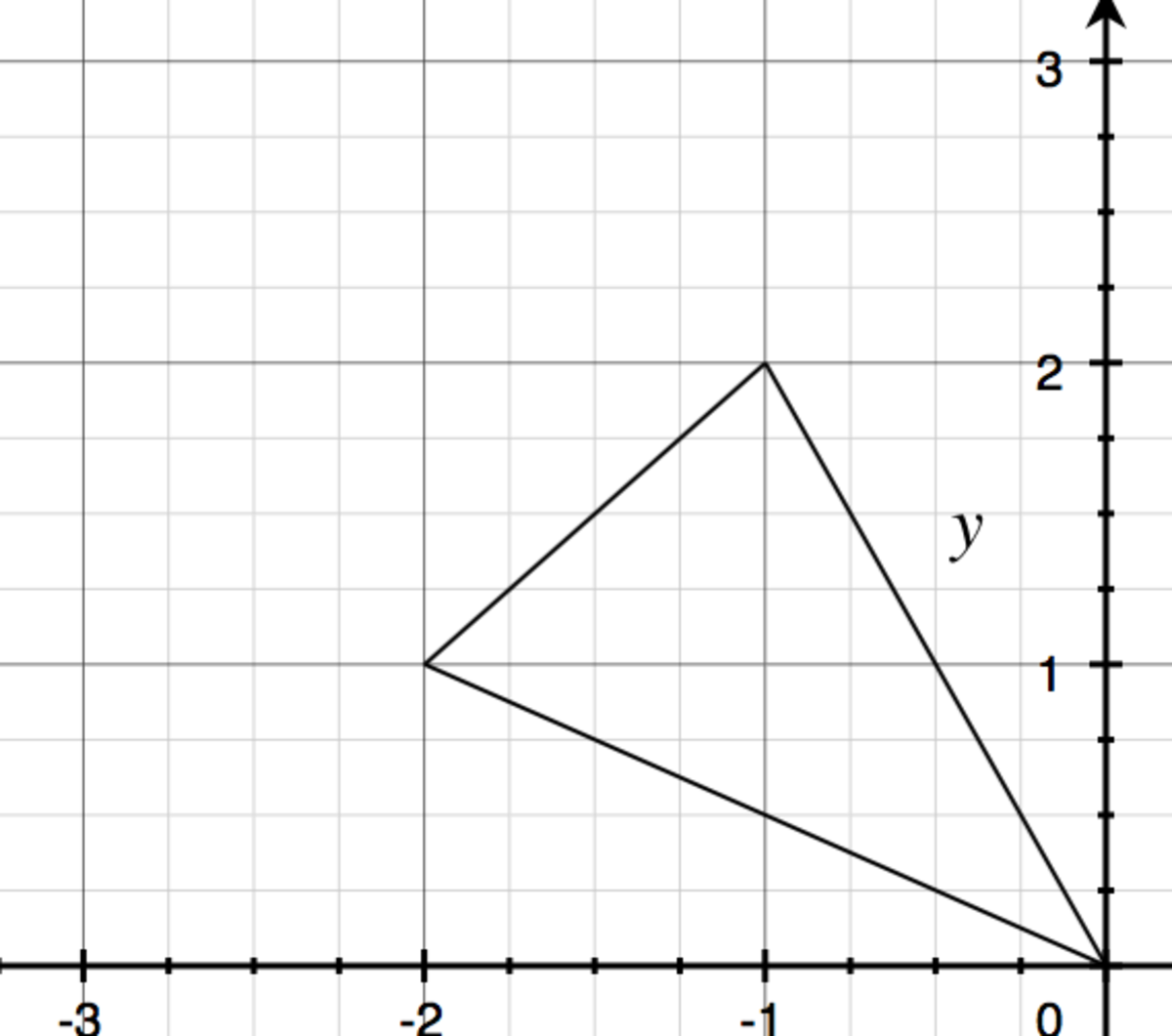
->
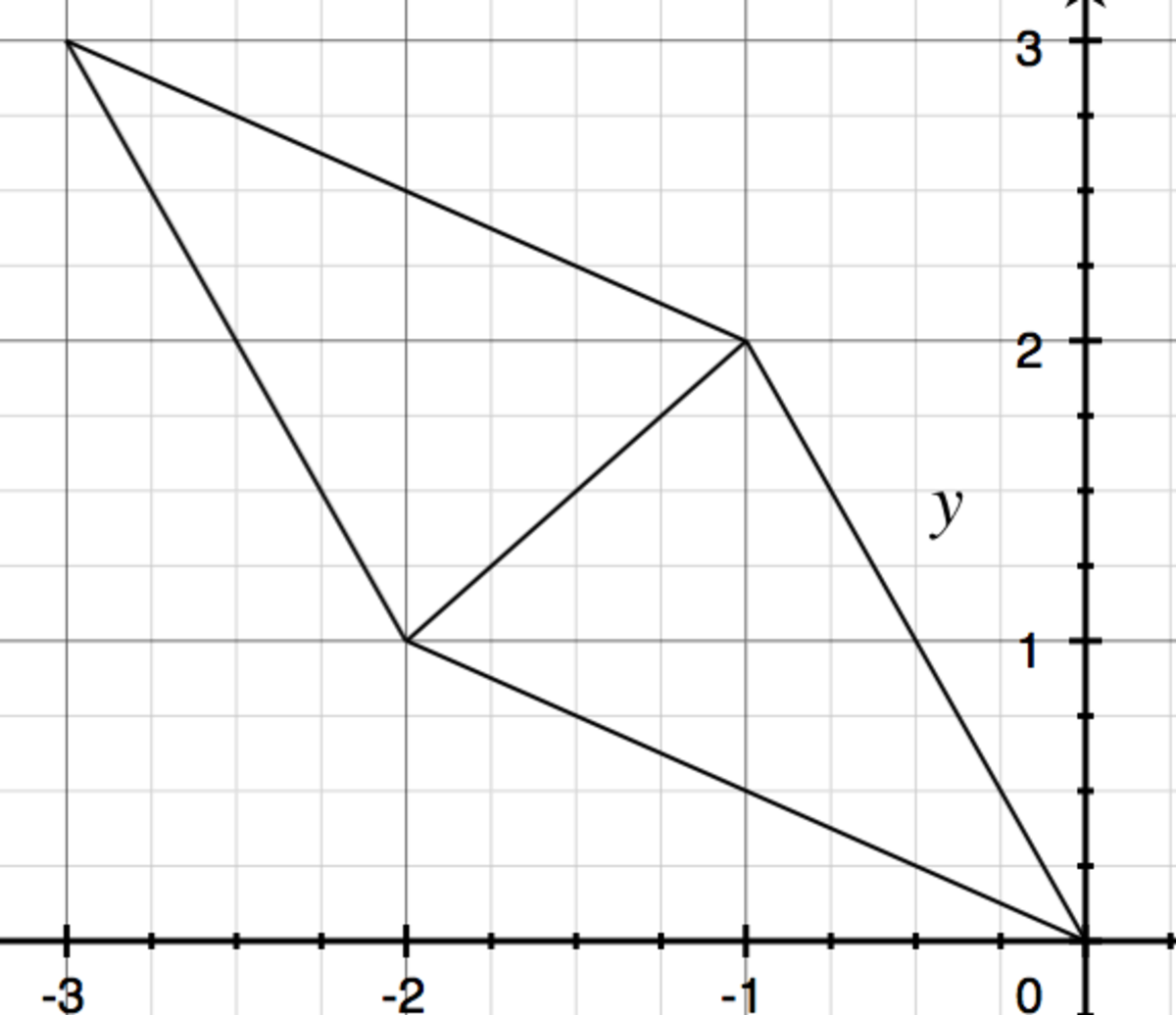A parallelogram is also a unit square for a linear system, in this case the system is
[
−
2
1
−
1
2
]
That means the area of a triangle is proportional to the determinant of that system. (the determinant is just the area of the unit square) In our example, that's -3.
So how does this help us?
To answer that, I'm going to have to go on a tangent on the transpose function. Functionally, it does this [ − 2 1 − 1 2 ] - > [ − 2 − 1 1 2 ]
the transpose function has two properties that we're interested in:
So the transpose function creates a parallelogram, which has two triangles, which have the same area as the original two triangles.
But these triangles are always going to be different ... unless the n the transpose function had to use was 0, in which case that would mean that there is no other triangle shape with the same area. But since the triangle area graphs are known to only have one global extrema, it must mean that a linear system that is its own transpose is inhabiting that extrema!
So when is a linear system its own transpose?
It turns out there's only one case.. when a matrix follows the pattern of [ a b b c ]
And here is where rotation comes into it. multiplying an arbitrary linear system, we find that we have the following formulas
[ c o s ( t ) s i n ( t ) − s i n ( t ) c o s ( t ) ] [ a b c d ] = [ a ∗ c o s ( t ) − b ∗ s i n ( t ) a ∗ s i n ( t ) + b ∗ c o s ( t ) c ∗ c o s ( t ) − d ∗ s i n ( t ) b ∗ s i n ( t ) + d ∗ c o s ( t ) ] c ∗ c o s ( t ) − d ∗ s i n ( t ) = a ∗ s i n ( t ) + b ∗ c o s ( t ) -> 0 = ( a + d ) ∗ s i n ( t ) + ( b − c ) ∗ c o s ( t )
You can go through and calculate the angle if you like, but we know that there will always exist some angle t that will cause the 1,2 and 2,1 element to equal the same thing under rotation, making it impossible for Tracy to improve the triangle further and forcing her to leave it alone.