Train route
Two villages (points B and C) are to receive a train connection to their neighboring city (point A), as shown in the diagram.
In order to save money when building the train route, only the connection with the shortest rail route is selected.
How many kilometers of rails must be laid? Round the result to the nearest integer.
Note : The railroad does not necessarily have to be built on the 30 km segments indicated in the diagram. A railroad switch can be built to allow a railroad to split into different paths.
The answer is 46.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
Not that I see your solution, I get for what you were asking, but this wasn't remotely clear to me from the wording of the problem.
How do we know that the optimal solution is for angle PAB to be 20 degrees?
I see people mostly working out complicated formulae to minimize in order to find the optimum. But this is a well-known class of problems, the optimum of which has 3 angles of 120° around point P. All you have to do is work out the sides of the 20°-120°-40° triangle.
Because the situation is symmetric, choose the origin at point A and run the x -axis along the angle bisector of ∠ C A B . The coordinates of B , C are ( a , ± b ) where a = 3 0 cos 2 0 ∘ and b = 3 0 sin 2 0 ∘ .
The shortest solution may a involve point P and three pieces of track A P , B P , C P . We don't exclude the possibility that two pieces of track suffice; in that case, we would simply have P = A . Let the coordinates of P = ( x , y ) . Symmetry suggests y = 0 (we can make this more precise later). The amount of rails needed is a function of x , ℓ ( x ) = x + 2 ( a − x ) 2 + b 2 . Minimizing this requires a zero derivative, i.e. 0 = d x d ℓ = 1 − ( a − x ) 2 + b 2 2 ( a − x ) . Multiply by the denominator, separate, and square to find ( a − x ) 2 + b 2 = ( 2 ( a − x ) ) 2 , 3 ( a − x ) 2 = b 2 , x = a − 3 b , ℓ = a + 3 b .
Substitute a = 3 0 cos 2 0 ∘ and b = 3 0 sin 2 0 ∘ to conclude ℓ ≈ 4 6 km.
Note that for this optimal solution, ∠ A P B = ∠ B P C = ∠ C P A = 1 2 0 ∘ .
I think I have lost track of which variables or side lengths you are using. where does x + 2*sqrt{(a-x)^2 - b^2} come from? more specifically, what do (a) and (b) represent?
I did something very similar, but I put the lenght of the rails as a function of the angle APC, it involved a lot of sines and got very hard to diferentiate so I had to resort to computation to find the answer, your way is a lot simpler. Well thought! =D
At the end should be L=a+sqrt(3)*b
Since △ A B C is an isosceles triangle, the minimum amount of track would form a Y-shape as shown below, where A D bisects ∠ A .
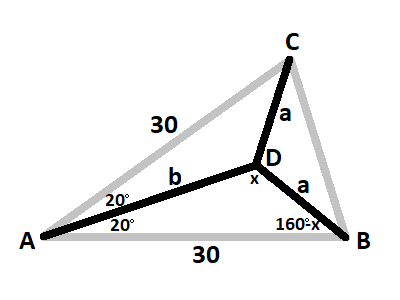
The total amount of track would be T = b + 2 a , where a = sin x 3 0 sin 2 0 ° and b = sin x 3 0 sin ( 1 6 0 ° − x ) according to the law of sines, so T = sin x 3 0 sin ( 1 6 0 ° − x ) + 6 0 sin 2 0 ° .
The minimum amount of track would be when T ’ = 0 , or when
sin 2 x ( sin x ) ( 3 0 cos ( 1 6 0 ° − x ) ( − 1 ) ) − ( 3 0 sin ( 1 6 0 ° − x ) + 6 0 sin 2 0 ° ) cos x = 0
− 3 0 sin x cos ( 1 6 0 ° − x ) − 3 0 sin ( 1 6 0 ° − x ) cos x − 6 0 sin 2 0 ° cos x = 0
− 3 0 ( sin x cos ( 1 6 0 ° − x ) + sin ( 1 6 0 ° − x ) cos x ) − 6 0 sin 2 0 ° cos x = 0
− 3 0 sin ( x + 1 6 0 ° − x ) − 6 0 sin 2 0 ° cos x = 0
− 3 0 sin 1 6 0 ° − 6 0 sin 2 0 ° cos x = 0
− 3 0 sin ( 1 8 0 ° − 2 0 ° ) − 6 0 sin 2 0 ° cos x = 0
− 3 0 sin 2 0 ° − 6 0 sin 2 0 ° cos x = 0
− 6 0 sin 2 0 ° cos x = 3 0 sin 2 0 °
cos x = − 2 1
x = 1 2 0 °
The minimum amount of track is therefore T = sin 1 2 0 ° 3 0 sin ( 1 6 0 ° − 1 2 0 ° ) + 6 0 sin 2 0 ° ≈ 4 6 .
The problem is basically asking for a point which has minimum total distance to A B and C. That's the Fermat Point of triangle. Denote it as P. It has three 120° angles when connected to the three vertexes (can be proved geometrically or physically). Triangle BAC being isosceles simplifies the calculation. By Law of Sines, we have sin120/30=sin20/PB=sin40/PA. So PA~=22.3 , PB~=11.8 , and hence total length of railway shall be PA+2PB ~=46 2017.12.27
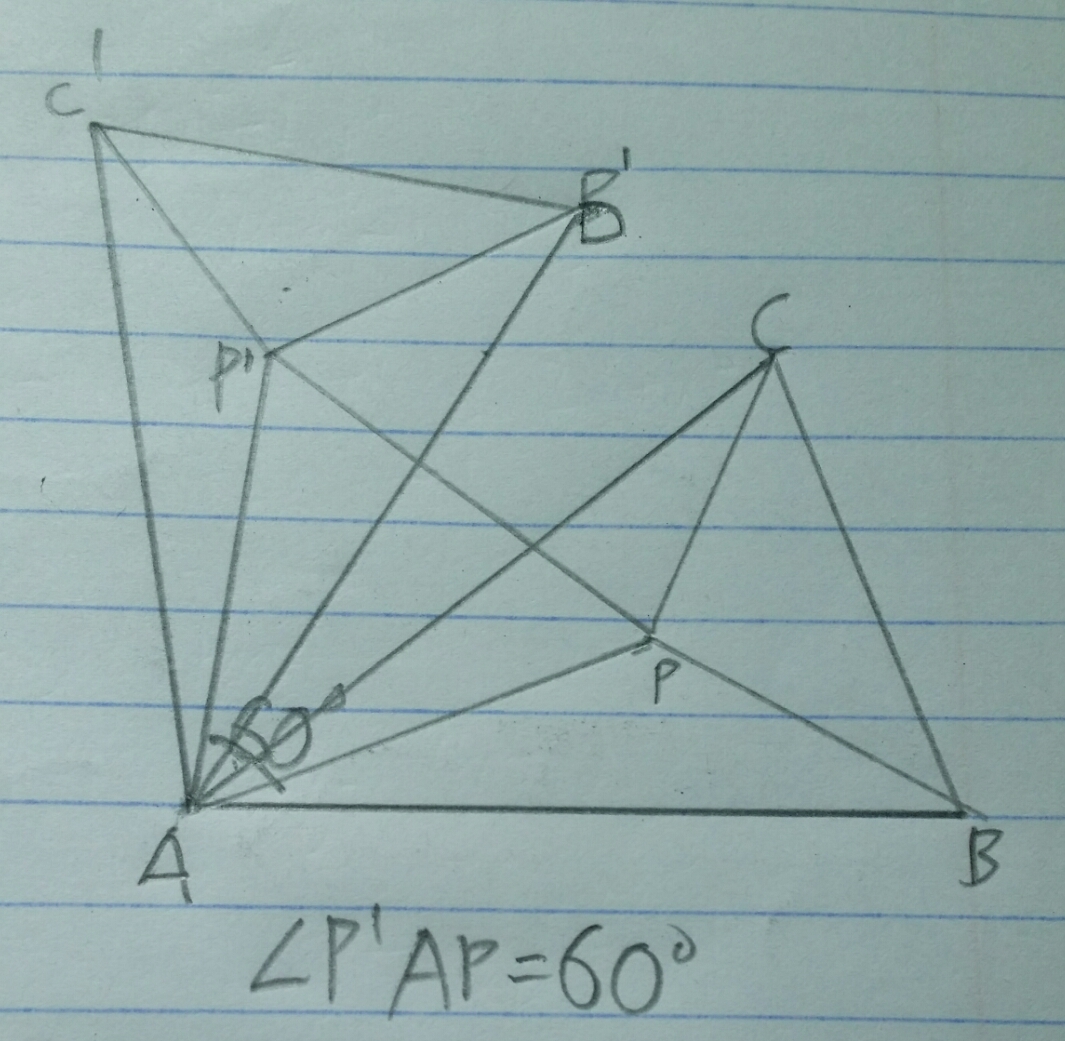 There exist a point
P
such that
A
P
+
B
P
+
C
P
achieve it's minimum value. We are finding the minimum value of
A
P
+
B
P
+
C
P
. Rotate triangle
A
B
C
and point
P
with
6
0
°
degree counterclockwise by centre
A
. Let the new image is triangle
A
B
′
C
′
and point
P
′
.
There exist a point
P
such that
A
P
+
B
P
+
C
P
achieve it's minimum value. We are finding the minimum value of
A
P
+
B
P
+
C
P
. Rotate triangle
A
B
C
and point
P
with
6
0
°
degree counterclockwise by centre
A
. Let the new image is triangle
A
B
′
C
′
and point
P
′
.
Note that A P = A P ′ and ∠ P A P ′ = 6 0 ° , so P P ′ = A P . Besides that, B ′ P ′ = B P . Hence, we can conclude that A P + B P + C P = P P ′ + B ′ P ′ + C P . P P ′ + B ′ P ′ + C P achieve its minimum value when B ′ C is a straight line, or B ′ A C is a triangle.
Hence, the required length is 3 0 2 + 3 0 2 − 2 × 3 0 2 × cos ( 6 0 ° + 4 0 ° ) = 4 5 . 9 6 . Hence, the answer is 4 6 .
For people like me who are bad at geometry:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
|
Yields:
1 2 |
|
Using basic trigonometry, we can find out that our points A , B , C can be placed in coordinate system in the following way:
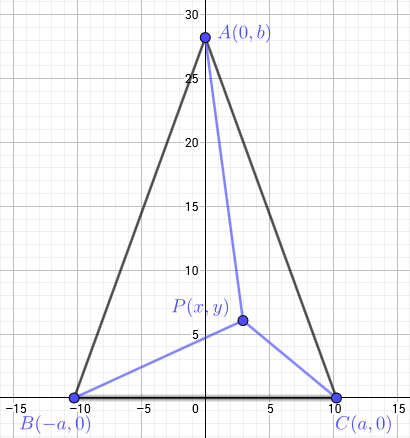
where a = 3 0 sin ( 2 0 ∘ ) , b = 3 0 cos ( 2 0 ∘ ) .
The blue lines are rails to be built, so we want to minimize their total length, which corresponds to minimizing the function f ( x , y ) = ( x − a ) 2 + y 2 + ( x + a ) 2 + y 2 + x 2 + ( y − b ) 2 .
Now, this would be extremely tedious to minimize by hand. Luckily, such a point P is a known center of a triangle - Fermat point . Following the construction given at Wikipedia, it is obvious that minimum of f occurs when x = 0 , so we can simplify the problem to minimizing g ( y ) = f ( 0 , y ) = 2 y 2 + a 2 + ( y − b ) 2 . Furthermore, it is obvious that minimum should occur for y ∈ [ 0 , b ] , and thus g simplifies to h ( y ) = 2 y 2 + a 2 + ( b − y ) . Taking derivative gives us h ′ ( y ) = y 2 + a 2 2 y − 1 and solving h ′ ( y ) = 0 gives us y = 3 a . Thus, the minimum distance is h ( a / 3 ) ≈ 4 5 . 9 6 2 7 ≈ 4 6 .
Let X be a set of points, where, for i ∈ { 1 , 2 , . . . , n } , x i ∈ X . Let ( x , y ) be the location of the rail switch. We wish to minimize the total distance D = ∑ d i = ∑ ( x − x i ) 2 + ( y − y i ) 2
For the sake of ease, we minimize the sum of squares of distances, D s :
D s = ∑ ( x − x i ) 2 + ( y − y i ) 2
We differentiate with respect to x :
∂ x D s = 2 ∑ ( x − x i ) = 0
Solving for x , we see that x = n 1 ∑ x i = x ˉ . Similar analysis shows that y = y ˉ . Computing these values gives us ( x ˉ , y ˉ ) = ( 1 7 . 6 6 , 6 . 4 2 8 ) . The total length of track is now simply the sum of the distances from this point to the points ( 0 , 0 ) , ( 3 0 , 0 ) , and ( 3 0 cos 4 0 , 3 0 s i n 4 0 ) , which yields approximately 46 km.
Note that this can be generlized to higher dimensions for larger sets of points.
By the triangle inequality, and the fact that the shortest distance between any two points is the straight line distance, we can say that the shortest rail will be consumed when a point in the triangle will have minimum sum of distances with the points A, B and C.
Every isolated system tends to acquire a minimum potential energy state.
Now, let us keep the triangle on a table, and poke holes at the points where A, B, and C lie. Now, we take three strings (length quite long), and join one end inside the triangle, and the other coming down from the holes, and we attach a mass M to all three. Leaving them isolated, they rearrange such that the sum of heights of the three masses from ground is minimized, because the gravitational potential energy is m g h .
This point minimizes our rail route, as the length of the strings was the same. Now, at the junction,vector sum of three equal forces is null, which means they are at 1 2 0 ∘ to each other.
With this information, we can easily calculate the distances by Sine Rule.
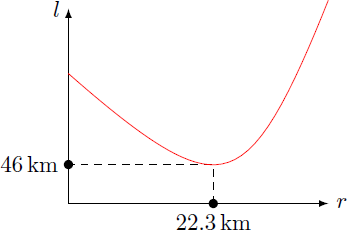
The connection vectors b = A B and c = A C between the city and the villages each have the same length b = c = 3 0 and an angle α = ∠ ( b , c ) = 4 0 ∘ . The idea is to lay a Y-shaped rail track in-between with a turnout in point P . Although this route is not optimal for the train service, the construction costs for the track can be minimized. The connection vector to point P equals r = ( r cos 2 α r sin 2 α ) The total length of the track results l = r + ∣ b − r ∣ + ∣ c − r ∣ = r + 2 ∣ b − r ∣ = r + 2 ( b − r cos 2 α ) 2 + r 2 sin 2 2 α = r + 2 b 2 + r 2 − 2 r b cos 2 α If we plot the function l ( r ) , we get a minimum at r ≈ 2 2 . 3 km and l ≈ 4 6 km .