Trains on a circular track
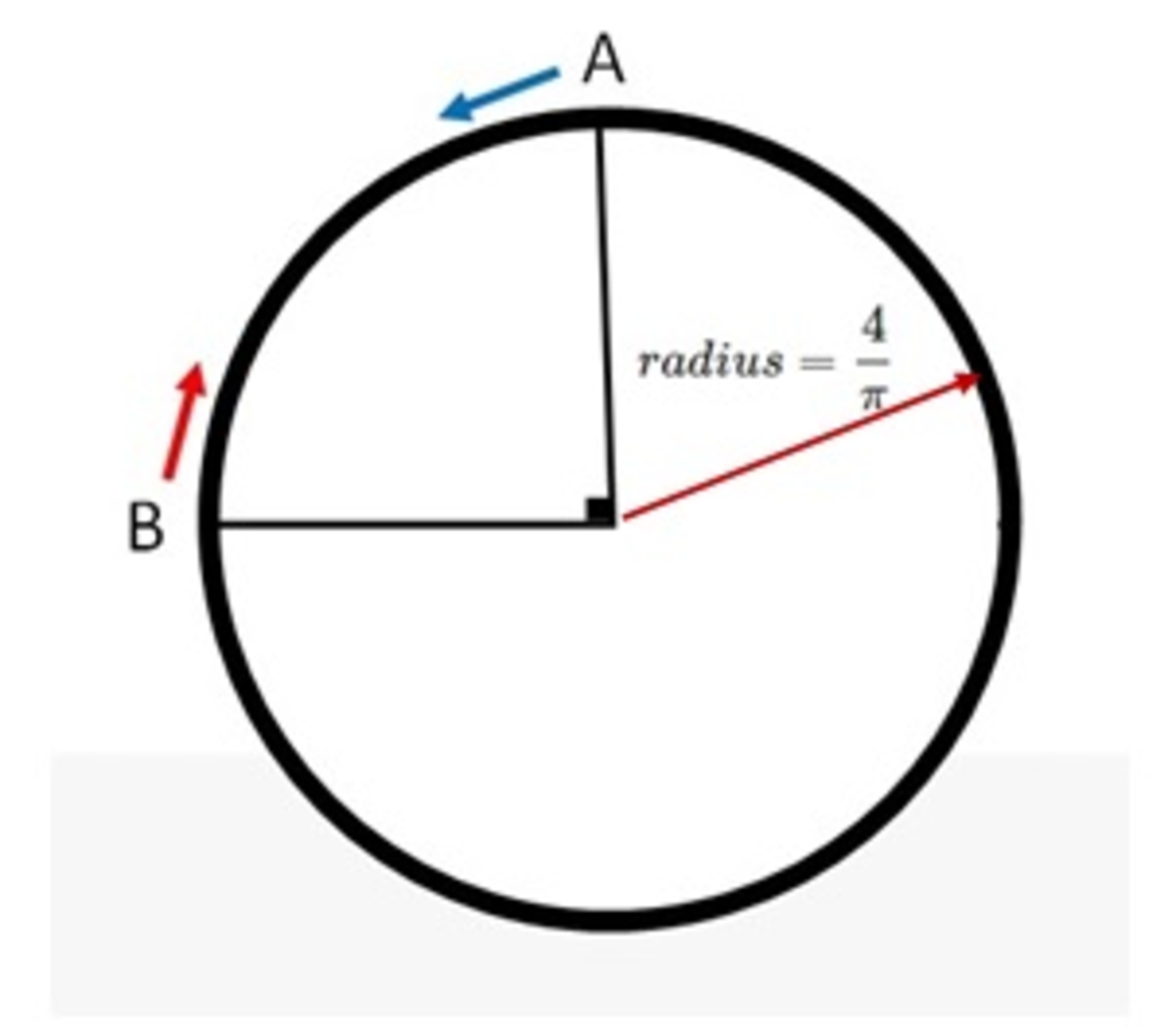
Two trains start moving toward each other at the same time from two points A and B with two different uniform speeds and as shown above. After meeting each other at some point between A and B, each of them continues to move in the same direction until they reach their initial stations. The train that departed from A arrived back at point A after 34 minutes, and the train that departed from B returned to point B after 54 minutes. What is the value of ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The distance between A and B = ( 2 π × r a d u i s ) / 4 = ( 2 ∗ 4 / 4 ) = 2
Assume that the two trains will meet after a distance D from point A after time = t . then
t = D / V a = ( 4 − D ) / V b -----------------(1)
The train from A will travel for a distance ( 8 − D ) to return to point A again and the train from B will travel distance = ( 6 + D ) to return to point B again.
using the given time from both trains.,
( 8 − D ) / V a = 3 4 / 6 0 ----------------------(2)
( 6 + D ) / V b = 5 4 / 6 0 ------------------(3)
solving (1), (2), and (3),
V a = 1 2 and V b = 8
V a / V b = 1 2 / 8 = 1 . 5