Transformation Complication
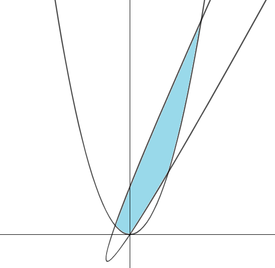
If the area of the blue region bounded by the graph and its image after the transformation matrix presented by can be expressed as , where are positive integers and , input as your answer.
The answer is 26.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First, I think the picture isn't quite right in that it was horizontally reflected.
Ok, let's get to the solution.
Step 1: Find the equation of the transformed graph x ′ = 2 x + y y ′ = 3 x + 2 y
The original equation: y = x 2
The transformed graph: 3 x + 2 y = ( 2 x + y ) 2
Step 2: Solve for points of intersection between these two graphs via simultaneous equations y = x 2 3 x + 2 y = ( 2 x + y ) 2 Which is relatively straightforward, giving us 4 coordinates: ( 0 , 0 ) , ( − 3 , 9 ) , ( 2 − 1 + ( 5 ) , 2 3 − ( 5 ) ) , ( 2 − 1 − ( 5 ) , 2 3 + ( 5 ) )
Step 3: Make y the subject in the equation of the transformed graph y = − 2 x ± 1 − x + 1
Step 4: Find multiples areas, which will be added/subtracted with each other to find the final area
Let the final area be X
Let A,B,C,D be these areas A = ∫ − 3 2 − 1 − 5 x 2 d x B = ∫ 2 − 1 − 5 0 − 2 x − 1 − x + 1 d x --> chose minus because looking at the lower curve C = ∫ 0 2 − 1 + 5 x 2 d x D = ∫ − 3 2 − 1 + 5 − 2 x + 1 − x + 1 d x --> chose plus because looking at the upper curve
Evaluating all 4 of these, we get A = 3 2 5 − 5 , B = 3 4 + 5 , C = 3 − 2 + 5 , D = 3 5 0 + 5
Step 5: Calculate the final area X = D − A − B − C = 3 2 3