Transformation of Roots!

We'll use the companion matrix (actually we've used the transpose of the companion matrix below, as the determinant of a matrix is equal to the determinant of it's transpose) of the polynomial $P(x)$ namely:

$A = \begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ -1 & 3 & 0 \end{pmatrix} \quad ,$

for which the characteristic polynomial is $\text{det}(xI-A) = x^3 - 3x + 1$ . For each integer $k \geq 1$ , the zeroes of the characteristic polynomial of $A^{k}$ are the $k^{th}$ powers of the zeroes of $P(x)$ . Taking this into account, we find that $Q(x) = \text{det}(xI-A^5)$ . It is an easy exercise to see that:

$A^5 = \begin{pmatrix} -3 & 9 & -1 \\ 1 & -6 & 9 \\ -9 & 28 & -6 \end{pmatrix} \quad .$

Thus we have $Q(x)$ as:

$Q(x) = \text{det}(xI-A^5) = \begin{vmatrix} x+3 & -9 & 1 \\ -1 & x+6 & -9 \\ 9 & -28 & x+6 \end{vmatrix} = x^3 +15x^2 -198x + 1$

Thus $\quad A=15, \quad B=-198, \quad C=1, \quad A+B+C = \boxed{-182}$ .

Let the roots of $P(x)$ be $a$ , $b$ and $c$ , therefore, the roots of $Q(x)$ are $a^5$ , $b^5$ and $c^5$ . By Vieta's formulas:

$\begin{cases} a + b + c & = 0 \\ ab + bc + ca & = -3 \\ abc & = -1 \end{cases} \quad \text{and} \quad \begin{cases} A = a^5+b^5+c^5 \\ B = a^5b^5 + b^5c^5 + c^5a^5 \\ C = a^5b^5c^5 \end{cases}$

\(\begin{array} {} a+b+c = 0 & = 0 \\ a^2+b^2+c^2 = (a+b+c)(a+b+c) - 2(ab+bc+ca) = 0-2(-3) & = 6 \\ a^3+b^3+c^3 = (0) (a^2+b^2+c^2) +3(a+b+c) + 3abc = 0+3(0) +3(-1) & = -3 \\ a^4+b^4+c^4 = 3(a^2+b^2+c^2) -(a+b+c) = 3(6) -(0) & = 18 \\ a^5+b^5+c^5 = 3(a^3+b^3+c^3) -(a^2+b^2+c^2) = 0+3(-3) -(6) & = -15 \end{array} \)

$\Rightarrow A = 15$

Let $\alpha = ab$ , $\beta = bc$ and $\gamma = ca$ , therefore, $B = a^5b^5 + b^5c^5 + c^5a^5 = \alpha^5 + \beta^5 + \gamma^5$ and, we have:

$\begin{cases} \alpha+\beta+\gamma = ab + bc + ca & = -3 \\ \alpha \beta + \beta \gamma + \gamma \alpha = ab^2c + abc^2 + a^2bc = abc(a+b+ c) & = 0 \\ \alpha \beta \gamma = (abc)^2 & = 1\end{cases}$

\(\begin{array} {} \alpha+\beta+\gamma = -3 & = -3 \\ \alpha^2+\beta^2+\gamma^2 = (-3)^2 -2(0) & = 9 \\ \alpha^3 + \beta^3 + \gamma^3 = -3(9) -0+3(1) & = -24 \\ \alpha^4 + \beta^4 + \gamma^4 = -3(-24) + (-3) & = 68 \\ \alpha^5 + \beta^5 + \gamma^5 = -3(69) + 9 & = -198 \end{array} \)

$\Rightarrow B = -198$

$C = -(abc)^5 =-(-1)^5 = 1$

$\Rightarrow A+B+C = 15-198+1 = \boxed{-182}$

i used an excel program to solve, i will explain: by vieta's: $P\begin{cases} \alpha+\beta+\gamma=0\\ \alpha\beta+\beta\gamma+\gamma\alpha=-3\\ \alpha\beta\gamma=-1 \end{cases} Q \begin{cases} A=-(\alpha^5+\beta^5+\gamma^5)\\ B=(\alpha\beta)^5+(\beta\gamma)^5+(\gamma\alpha)^5\\ C=-(\alpha\beta\gamma)^5 \end{cases}$ i hope you all know newtons sum, it pretty basic to find A using newtons sum: 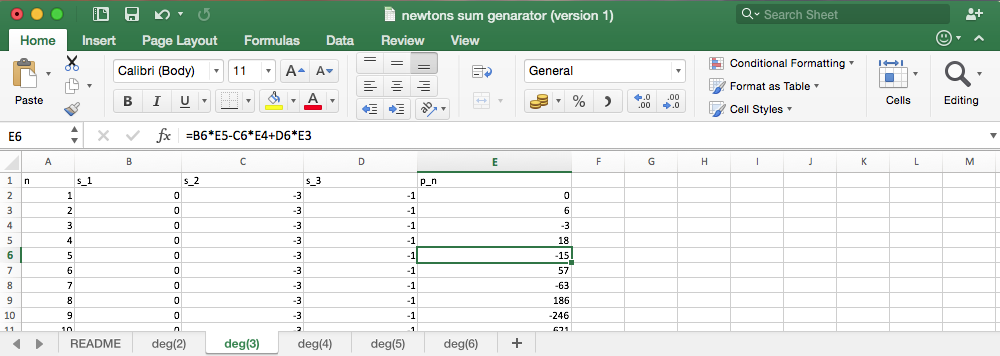$A=-(\alpha^5+\beta^5+\gamma^5)=-(-15)=15$ and $C=-(-\alpha\beta\gamma)^5=-(-1)^5=1$ B is the rather fun part. if we consider roots to be, $\alpha\beta,\beta\gamma,\gamma\alpha$ then $\begin{cases} s_1=\alpha\beta+\beta\gamma+\gamma\alpha=-3\\ s_2=\alpha\beta(\beta\gamma)+\beta\gamma(\gamma\alpha)+\gamma\alpha(\alpha\beta)=\alpha\beta\gamma(\alpha+\beta+\gamma)=-1(0)=0\\ s_3=\alpha\beta(\beta\gamma)(\gamma\alpha)=(\alpha\beta\gamma)^2=(-1)^2=1 \end{cases}$ putting these values: 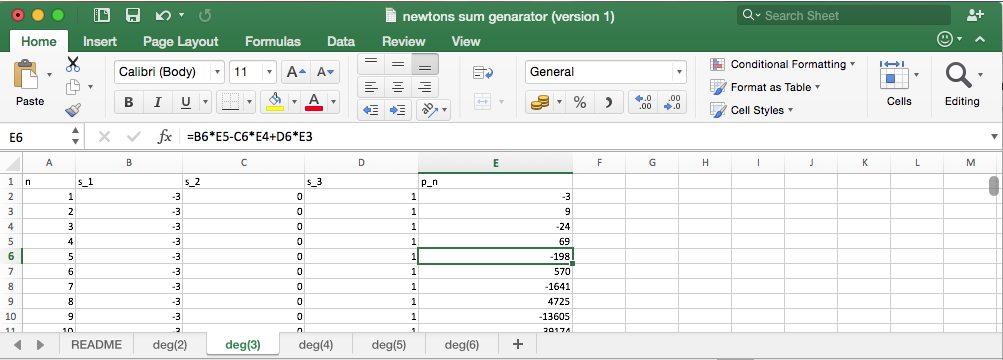hence $B=(\alpha\beta)^5+(\beta\gamma)^5+(\gamma\alpha)^5=-192$ and $A+B+C=15-192+1=\boxed{-182}$

I don't think I am adding anything new, but here is my proof as I obtained it before reading all your interesting solutions. Let $x_{1}, x_{2}, x_{3}$ be the roots of $P(x)$ . Then we define $S_{k}=x_{1}^{k} + x_{2}^{k}+x_{3}^{k}$ where $k$ is any non-negative integer number. Using the Newton's sums we obtain the following

\(\begin{array} {} S_{0}=3\\S_{1}=0\\S_{2}=0. S_{1}+3*2=6\\S_{3}=0*S_{2}+3*S_{1}-S_{0}=-3\\S_{4}=0*S_{3}+3*S_{2}-S_{1}=18\\S_{5}=0*S_{4}+3*S_{3}-S_{2}=-15\\S_{6}=0*S_{5}+3*S_{4}-S_{3}=57\\S_{7}=0*S_{6}+3*S_{5}-S_{4}=-63\\S_{8}=0*S_{7}+3*S_{6}-S_{5}=186\\S_{9}=0*S_{8}+3*S_{7}-S_{6}=-246\\S_{10}=0*S_{9}+3*S_{8}-S_{7}=621\end{array}\)

Obviously $A=-S_{5}=15$ and $C=-(x_{1}^{5}*x_{2}^{5}*x_{3}^{5}) =-(x_{1}* x_{2}* x_{3})^5=-(-1)^5=1.$ Now let us find B

$B=x_{1}^{5}x_{2}^{5}+x_{1}^{5}x_{3}^{5}+x_{2}^{5}x_{3}^{5}=\frac{1}{2}(S_{5}^2-S_{10})=\frac{1}{2}((-15)^2-621)=-198$ So $A+B+C=15+(-198)+1=-182.$