Transformer (8-13-2020)

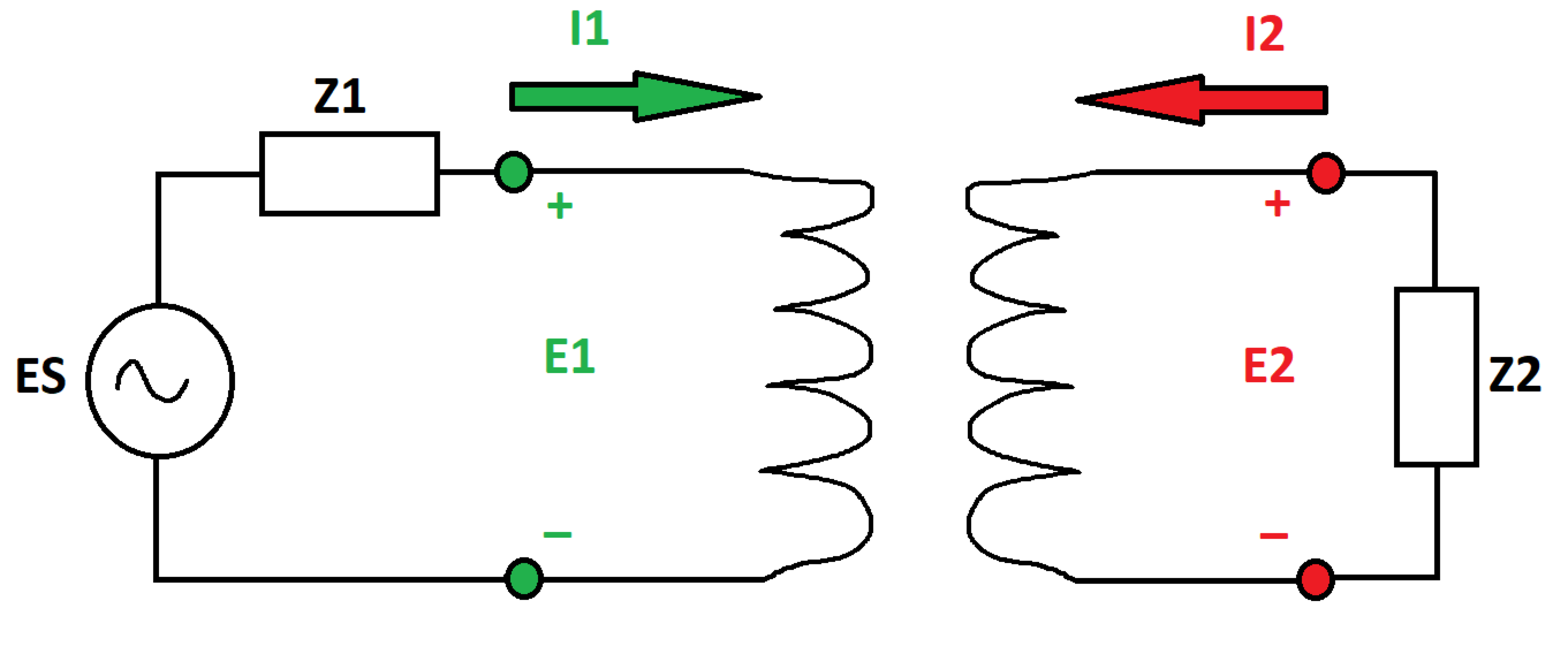
A transformer is governed by the following equations:

$E_1 = Z_S I_1 + Z_M I_2 \\ E_2 = Z_M I_1 + Z_S I_2$

In the equations, $E_1$ and $E_2$ are the terminal voltages and $I_1$ and $I_2$ are the terminal currents (note the polarity conventions in the diagram). $Z_S$ and $Z_M$ are the transformer winding self and mutual impedances.

An AC voltage source with internal voltage $E_S$ and internal impedance $Z_1$ is connected across the first set of terminals, and an impedance $Z_2$ is connected across the second set of terminals. Let $Z_2$ be purely resistive $(Z_2 = R + j 0)$ .

What is the limiting value of the magnitude of $E_1$ as $R$ approaches zero?

Bonus: What would the answer be if the transformer were ideal?

Details and Assumptions:
1) $E_S = 10 + j 0$
2) $Z_1 = 2 + j 5$
3) $Z_S = 0 + j 10$
4) $Z_M = 0 + j 5$
5) Consider all quantities to be complex numbers. The quantity $j$ is the imaginary unit