Transforming the Ellipse
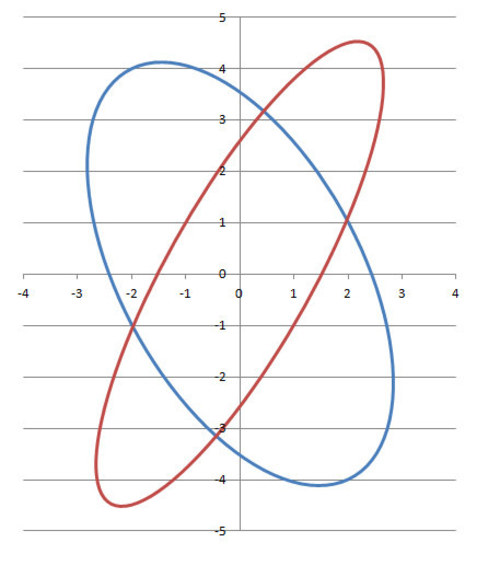 Given an ellipse (blue) with its semi-minor axis along the vector
, and its semi-major axis along the vector
. The ellipse is transformed by multiplying the position vector of each of its points by a matrix
, which is given by
Given an ellipse (blue) with its semi-minor axis along the vector
, and its semi-major axis along the vector
. The ellipse is transformed by multiplying the position vector of each of its points by a matrix
, which is given by
The resulting curve is another ellipse (red). Find the length of semi-major axis of the transformed ellipse. (To three decimal places)
This problem is original.
The answer is 5.072.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We are given an ellipse with semi-minor axis = (2, 1) and semi-major axis = (-2, 4). Hence, points on this ellipse can be written as
X = cos ( t ) [ 2 1 ] + sin ( t ) [ − 2 4 ]
where X = [ x , y ] T
In compact form,
X = [ 2 1 − 2 4 ] [ cos ( t ) sin ( t ) ]
Now each position vector is pre-multiplied by the matrix A, hence define Y as
Y = A X = [ 0 . 5 − 0 . 2 5 0 . 7 5 1 ] [ 2 1 − 2 4 ] [ cos ( t ) sin ( t ) ]
Performing the matrix multiplication, this results in
Y = [ 1 . 7 5 0 . 5 2 4 . 5 ] [ cos ( t ) sin ( t ) ]
Solving for the vector of the cosine and sine in terms of Y, by matrix inversion, we get
[ cos ( t ) sin ( t ) ] = 6 . 8 7 5 1 [ 4 . 5 − 0 . 5 − 2 1 . 7 5 ] Y
Now since
cos ( t ) 2 + sin ( t ) 2 = [ cos ( t ) sin ( t ) ] [ cos ( t ) sin ( t ) ] = 1
It follows that
Y T B Y = 1 . . . . . . . . . . . . . . . . ( ∗ )
where
B = 6 . 8 7 5 2 1 [ 4 . 5 − 2 − 0 . 5 1 . 7 5 ] [ 4 . 5 − 0 . 5 − 2 1 . 7 5 ]
Therefore,
B = 6 . 8 7 5 2 1 [ 2 0 . 5 − 9 . 8 7 5 − 9 . 8 7 5 7 . 0 6 2 5 ]
Now it is known that the length of the semi-minor and semi-major axis for the ellipse described by equation (*) are the square roots of reciprocals of the eigenvalues of matrix B . Since this is a 2 x 2 matrix, it is very easy to find the eigenvalues; they are simply the roots of this equation,
( x − 2 0 . 5 ) ( x − 7 . 0 6 2 5 ) − ( 9 . 8 7 5 ) 2 = 0
divided by the constant ( 6 . 8 7 5 ) 2 . The above quadratic equation becomes,
x 2 − 2 7 . 5 6 2 5 x + 4 7 . 2 6 5 6 2 5 = 0
By the quadratic formula,
x 1 = 1 . 8 3 7 3 2 9 9 3 3
x 2 = 2 5 . 7 2 5 1 7
Therefore, the eigenvalues are
λ 1 = 1 . 8 3 7 3 2 9 9 3 3 / ( 6 . 8 7 5 ) 2 = 0 . 0 3 8 8 7 2 4 3 4
λ 2 = 2 5 . 7 2 5 1 7 / ( 6 . 8 7 5 ) 2 = 0 . 5 4 4 2 6 8
Hence the length of the semi-major axis is
a = 0 . 0 3 8 8 7 2 4 3 4 1 = 5 . 0 7 2