Transforming Triangle 2
If Brilli the Ant is inside an equilateral triangle and 5 , 3 5 3 , and 1 0 3 7 units away from its vertices, how many units long is one side of the equilateral triangle?
The answer is 65.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
If only I had noticed the right triangle I could have avoided using the inverse law of cosines.
I found the smallest angle of the triangle using inverse law of cosines. Then I expanded it by 60 (as you solved the inspiration problem) and used the law of cosines on this new angle. Same result but more work.
The more "natural" way (and commonly used in olympiad problems) to see this is to consider an anticlockwise rotation of 6 0 ∘ about Q that brings P to P ′ . Then P P ′ Q is an isosceles triangle with vertex angle 6 0 ∘ , hence is equilateral. So P P ′ S is a triangle with side lengths 5 , 3 5 3 , 1 0 3 7 , hence is a right triangle.
This allows us to generalize to the general case (as does your approach), where we might not have a right triangle. We can calculate cos ∠ Q P S = cos ( ∠ S P P ′ + 6 0 ∘ ) , and have cos ∠ S P P ′ from the side lengths of the triangle.
Is there an unstated assumption in the problem?
I worked in the complex plane and set one vertex at (5,0) and then set up equations which I (well... mathematica actually) could easily solve numerically for the other two vertices. I thus found TWO solutions for the side length (depending on the initial estimates). One is indeed the lovely solution 65, and the other one was 56.3471. I presume in this case Brilli is OUTSIDE the triangle!
Log in to reply
You're right! I added the restriction that Brilli has to be inside the equilateral triangle.
Good catch. With the rotation argument (and placing the point outside the triangle), we get that the other length is
5 2 + ( 3 5 3 ) 2 + 2 ⋅ 5 ⋅ 3 5 3 cos 1 5 0 ° = 5 6 . 3 5 .
Hint: I will leave you to figure out why it's a "+". When you work through the proof, it should become obvious.
Log in to reply
For the point outside the triangle, the rotation method shows us that we subtract 6 0 ° instead of adding it, so cos ∠ Q P S = cos ( ∠ S P P ′ − 6 0 ° ) = cos ( 9 0 ° − 6 0 ° ) = cos 3 0 ° = − cos 1 5 0 ° , which makes a "+" when inserted in the law of cosines.
Slight typo in the last equation. It should be
5 2 + ( 3 5 3 ) 2 − 2 ⋅ 5 ⋅ 3 5 3 cos 1 5 0 ° = 6 5 .
Let the side length of the equilateral triangle be a and the coordinates of the top, left and right vertices be ( 0 , 2 3 a ) , ( − 2 1 a , 0 ) , and ( 2 1 a , 0 ) respectively, and the coordinates where Brilli is ( x , y ) . Then by Pythagorean theorem :
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ ( x − 0 ) 2 + ( y − 2 3 a ) 2 = 5 2 ( x + 2 1 a ) 2 + ( y − 0 ) 2 = ( 1 0 3 7 ) 2 ( x − 2 1 a ) 2 + ( y − 0 ) 2 = ( 3 5 3 ) 2 ⟹ x 2 + y 2 − 3 a y + 0 . 7 5 a 2 = 2 5 ⟹ x 2 + a x + 0 . 2 5 a 2 + y 2 = 3 7 0 0 ⟹ x 2 − a x + 0 . 2 5 a 2 + y 2 = 3 6 7 5 . . . ( 1 ) . . . ( 2 ) . . . ( 3 )
From ( 2 ) − ( 3 ) : ⟹ 2 a x = 2 5 ⟹ a x = 1 2 . 5 . . . ( 4 )
From ( 2 ) + ( 3 ) : ⟹ 2 x 2 + 0 . 5 a 2 + 2 y 2 = 7 3 7 5 ⟹ x 2 + y 2 = 3 6 8 7 . 5 − 0 . 2 5 a 2 . . . ( 5 )
From ( 2 ) − ( 1 ) : ⟹ a x + 3 a y − 0 . 5 a 2 = 3 6 7 5 ⟹ 3 a y = 3 6 6 2 . 5 + 0 . 5 a 2 . . . ( 6 )
Therefore, we have:
( 3 a x ) 2 + ( 3 a y ) 2 3 a 2 ( x 2 + y 2 ) 3 a 2 ( 3 6 8 7 . 5 − 0 . 2 5 a 2 ) = ( 1 2 . 5 3 ) 2 + ( 3 6 6 2 . 5 + 0 . 5 a 2 ) 2 = 4 6 8 . 7 5 + 1 3 4 1 3 9 0 6 . 2 5 + 3 6 6 2 . 5 a 2 + 0 . 2 5 a 4 = 1 3 4 1 4 3 7 5 + 3 6 6 2 . 5 a 2 + 0 . 2 5 a 4 ( 5 ) : x 2 + y 2 = 3 6 8 7 . 5 − 0 . 2 5 a 2
⟹ a 4 − 7 4 0 0 a 2 + 1 3 4 1 4 3 7 5 ( a 2 − 4 2 2 5 ) ( a 2 − 3 1 7 5 ) = 0 = 0
⟹ a = { 6 5 5 1 2 7
Since 5 1 2 7 < 3 5 3 < 1 0 3 7 , the answer is a = 6 5 .
I solved it as an algebra problem in 3 unknowns: the x and y coordinates of Brilli and s , the length of the side of the equilateral triangle with vertices at { 0 , 0 } , s { 2 1 , 2 3 } and s { 1 , 0 } . Unfortunately, there are two solutions. On the basis that the problem implicitly specified an integer side length and that Brilli was inside the triangle, I selected the 65 side length as the submitted solution. The two solutions are: { { s → 6 5 , x → 1 3 4 2 5 , y → 1 3 3 8 5 3 } , { s → 5 1 2 7 , x → 1 2 7 3 2 0 , y → 3 5 0 1 2 7 3 } } .
Yes, s = 5 1 2 7 would be a solution if Brilli was outside the triangle.
Great solution!
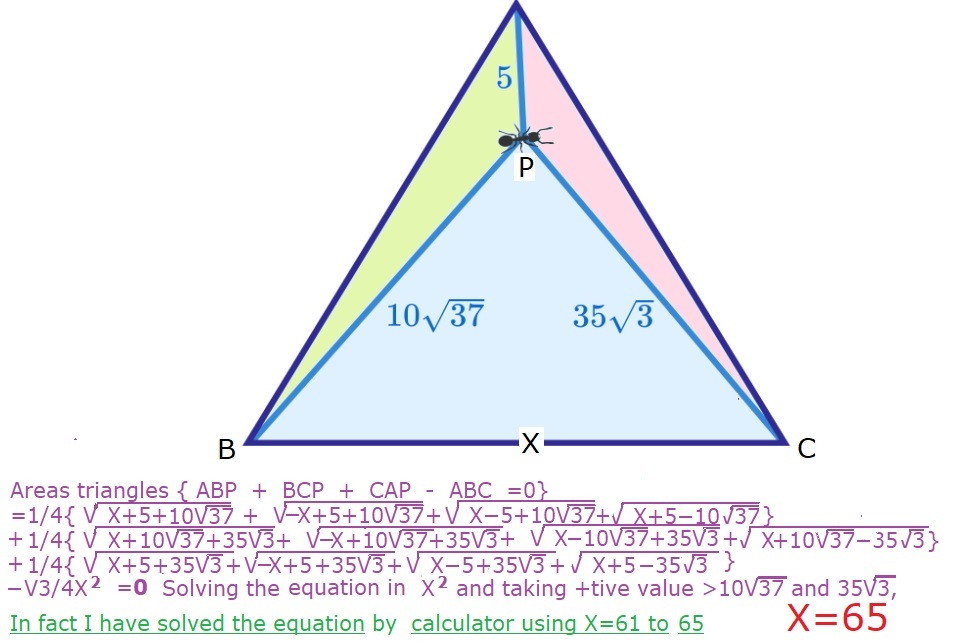
Assume x as the side.
Write Hero's formula for the areas of the three tangles.
Sum of this three formulas =
4
3
∗
x
2
.
Solving x=65 is only greater than
1
0
∗
3
5
,
a
n
d
3
5
∗
3
.
This is a great, unique solution! Thanks for sharing!
Let x be the length of one side of the equilateral triangle.
Let θ be the angle between sides of length 5 and 3 5 3 .
By rule of cosines, we have,
x 2 = 5 2 + ( 3 5 3 ) 2 − 2 × 3 5 3 × 5 × cos θ
We have that the three given lengths together form the side of a right-angled triangle, Since
5 2 + ( 3 5 3 ) 2 = ( 1 0 3 7 ) 2 .
Therefore in the new triangle formed from the Inspiration Problem we have that the angle between sides of length 5 and 3 5 3 = 9 0 ∘ . This implies (from answer to Inspiration Problem ), that θ = 1 5 0 ∘
Hence the first equation yields x 2 = 5 2 + ( 3 5 3 ) 2 − 2 × 3 5 3 × 5 × cos 1 5 0 ∘ = 2 5 + 3 6 7 5 − 2 × 3 5 3 × 5 × ( − cos ( 3 0 ∘ ) ) = 2 5 + 3 6 7 5 + 5 2 5 = 4 2 2 5
⟹ x = 6 5
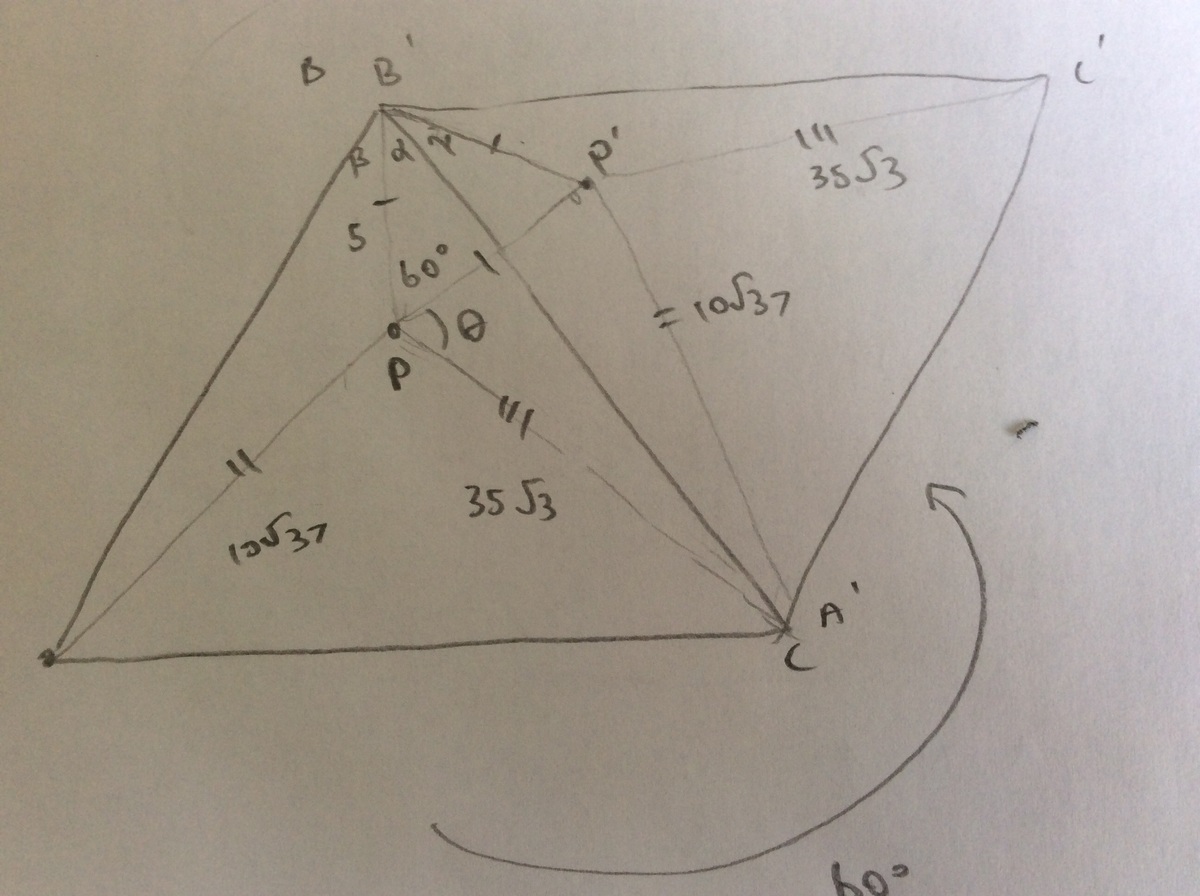
Consider the original triangle ABC, rotate it counter clockwise 60 degrees to form the corresponding points A'B'C' Now γ = β upon rotation, so α + γ = α + β = 60° From which we can deduce PP'B is an equilateral triangle so PP' = BP = 5 Using the Cosine Rule, ∠BPP' turns out to be 90° so ∠BPC = 150° and the length of a side of the equilateral triangle BC = 65 from the Cosine Rule.
This is an inspiration from a Coffin problem
Draw triangle
A
F
C
≅
A
E
B
,
∠ E A F = ∠ E A C + ∠ C A F = ∠ E A C + ∠ B A E = ∠ B A C = 6 0 ∘ → Triangle EAF is equilateral triangle. E F = F A = A E = 5 units.
Noted that E F 2 + E C 2 = F C 2 , by converse of Pythagorean theorem, ∠ F E C = 9 0 ∘
Using cosine rules, we have A C 2 = A E 2 + E C 2 − 2 A E ⋅ E C cos ( 6 0 ∘ + 9 0 ∘ ) = 4 2 2 5
hence A C = 6 5
Apply Pythagoras theorem:
Let a is horizontal distance form the vertical symmetry line, b is vertical distance from apex to Brilli.
((1/2)x + a)^2 + ((1/2)x√3 – b)^2 = (35√3)^2, ...........(1)
((1/2)x - a)^2 + ((1/2)x√3 – b)^2 = (10√37)^2, ...........(2)
a^2 + b^2 = 5^2. ...........(3),
Substract eqs(1) by eqs(2), we get 2xa = -25, or a = (-25)/(2x) ,
Add eqs(1) to eqs(2), we get 2x^2 + 50 - 2√3xb = 7375, or b = - (7325-2x^2)/(2√3x)
Substitute a, and b to eqs(3) and simplify, then we get
x^4 -7400 x^2+ 13414375 = 0, then x^2= (7400±1050)/2 , or x=65
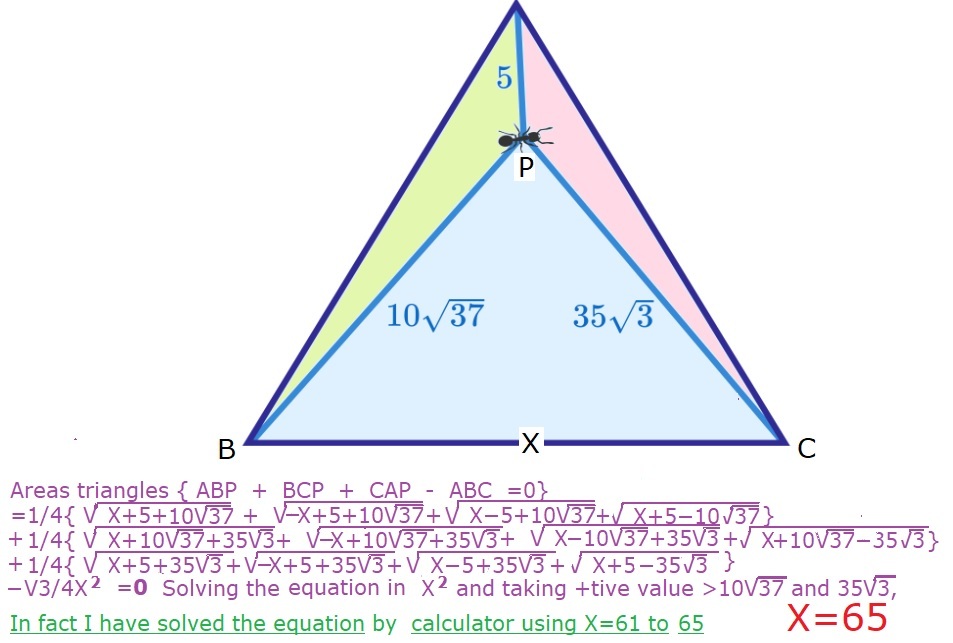
From the inspiration problem , we discovered that if P is a point inside an equilateral triangle △ Q R S , then equilateral triangles can be taken out of △ Q R S and the remaining triangles can be rearranged to make a triangle with double the sides of P Q , P R , and P S as shown below, which means that ∠ Q P R , ∠ Q P S , and ∠ R P S are exactly 6 0 ° more than corresponding angles in the non-equilateral triangle.
In this case, double P Q , P R , and P S are 1 0 , 7 0 3 , are 2 0 3 7 , and since 1 0 2 + ( 7 0 3 ) 2 = ( 2 0 3 7 ) 2 , these form a right triangle where the angle between 1 0 and 7 0 3 is 9 0 ° . Therefore, the angle between 5 and 3 5 3 near Brilli the Ant is 9 0 ° + 6 0 ° = 1 5 0 ° , and using the law of cosines, the third side (and also the side of the equilateral triangle) solves to 5 2 + ( 3 5 3 ) 2 − 2 ⋅ 5 ⋅ 3 5 3 cos 1 5 0 ° = 6 5 .