Transforming Triangle

Geometry Level 2

In an equilateral triangle $\triangle QRS$ , you draw a point $P$ inside of it. Afterwards, you connect $P$ to the three vertices of the triangle. Suppose you already know the magnitude of the two angles (called $\angle x$ and $\angle y$ ) as shown below. If you were to take the line segments $\overline{PQ}$ , $\overline{PR}$ , and $\overline{PS}$ and put them together to form a new triangle $\triangle TUV$ , is it possible to figure out the angle measurements of the new triangle?

Note: Diagrams are not to scale

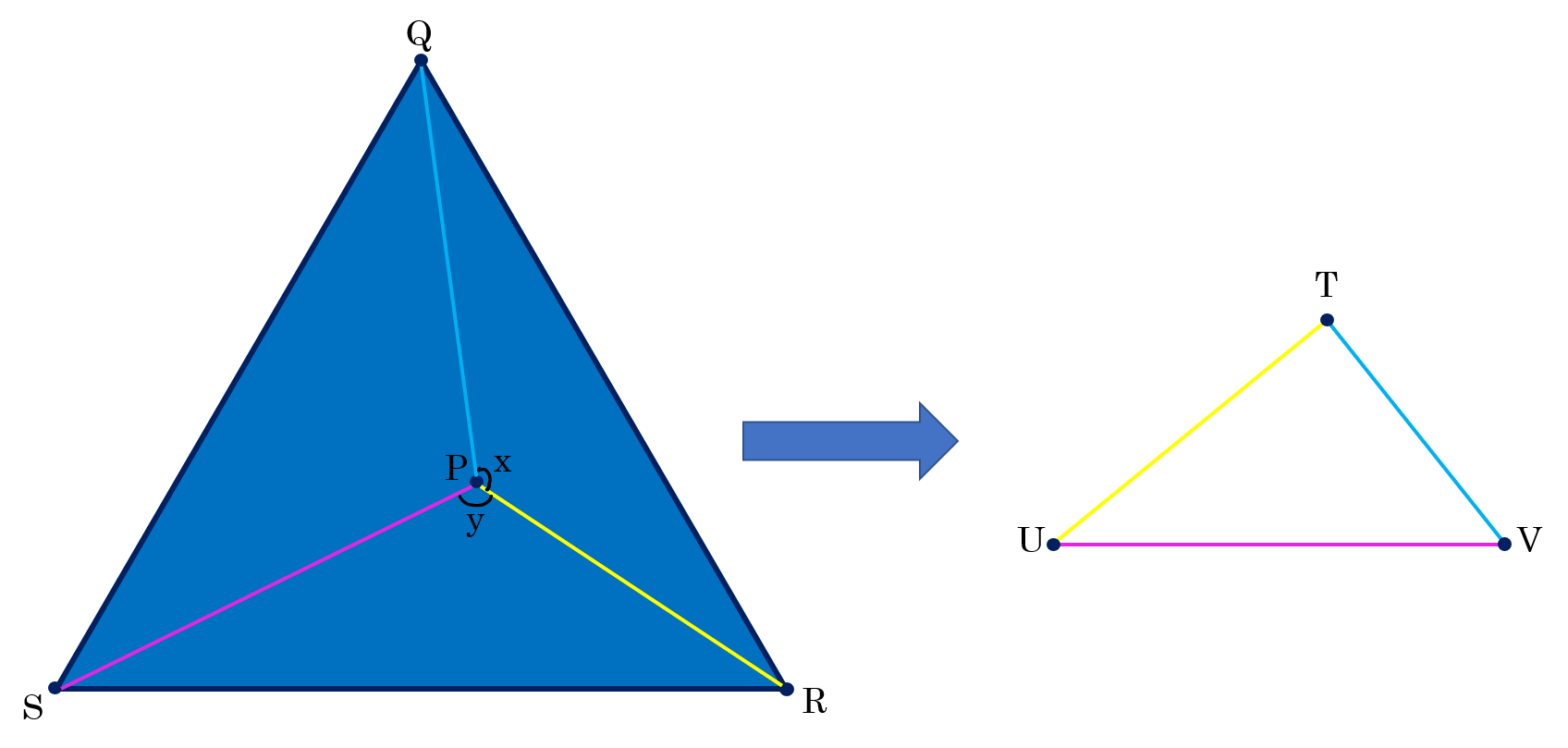
Bonus: If $\angle x = 76^{\circ}$ and $\angle y = 54^{\circ}$ , then what are the values for $\angle T$ , $\angle U$ , and $\angle V$ ?

Yes No Insufficient information

4 solutions

David Vreken
Jan 10, 2019

Equilateral triangles can be taken out of $\triangle QRS$ , and then the remaining triangles can be rearranged to make a triangle with double the sides of $PQ$ , $PR$ , and $PS$ , except for a hexagon in the center with each angle being $120°$ , as shown below, which by similarity would have the same angles as $\triangle TUV$ .

This means the angles in $\triangle TUV$ are all exactly $60°$ less than $\angle x$ , $\angle y$ , and $\angle QPS$ .

Therefore, if $\angle x$ and $\angle y$ are known, it is possible to determine the angle measurements of $\triangle TUV$ .

"the remaining triangles can be rearranged to make a triangle with double the sides of PQ, PR, and PS", may you prove it? (or, explain it?)

Ong Zi Qian - 2 years, 4 months ago

The picture in my solution explains how this can be done, where the colors of the first triangle match up with the colors of the second triangle.

David Vreken - 2 years, 4 months ago

If the solution is correct, y will never be 54

Ong Zi Qian - 2 years, 4 months ago

Yes, the bonus question of x = 76 and y = 54 would actually place the point outside the triangle, and not inside the triangle as originally asked.

David Vreken - 2 years, 4 months ago

For given angles x=76 and y=54 Their sum is 130 Therefore, you can't make even a triangle QRS with the point P inside the triangle. It will lie outside

Vikram Karki - 1 year, 1 month ago

How do you say "the hexagon in the center with each angle 120"? Isn't the angles of the hexagon depends on the "p" point?

Hiviru Palihena - 11 months, 2 weeks ago

If you look at the second picture, the pink base has a purple and blue triangle, which in the first picture made up $\angle S$ , an angle in an equilateral triangle which must be $60°$ . So the angle of the white hexagon near the pink base in the second picture is $180° - 60° = 120°$ , independent of $P$ . A similar argument can be made for each hexagon angle.

David Vreken - 11 months, 2 weeks ago

Thanks I got it and I understood your whole explanation. Seriously your explanation is creative than others.

Hiviru Palihena - 10 months, 2 weeks ago

Adrash Singh
Mar 21, 2019

Rotating triangle SQR on R point.
Let angle PRS =angle P'RS'=t and angle QRS=angle Q'RS' =60 (equilateral triangle) so , angle PRQ=60-t then angle PRP'=angle PRQ + angle P'RS' =60-t+t=60

--JOIN PP' ---Triangle PP'R IS AN EQUILATERAL TRIANGLE , because angle PRP'=60 and PR=P'R, so angle PP'R =angle P'PR. so angle PP'R +angle P'PR+60=180. by solving this equation we find that all angles are 60 degree . So ,Triangle PP'R IS AN EQUILATERAL TRIANGLE. So, PP'S is the desired triangle. So for angle X =76 angleY=54 {T=16 , U=-6 ,V=170} .
But it is not possible to construct a triangle with these 3 values.X and Y must be greater than 60 degrees and the sum of X and Y must be smaller than 300. I tried to construct a triangle and the result is this

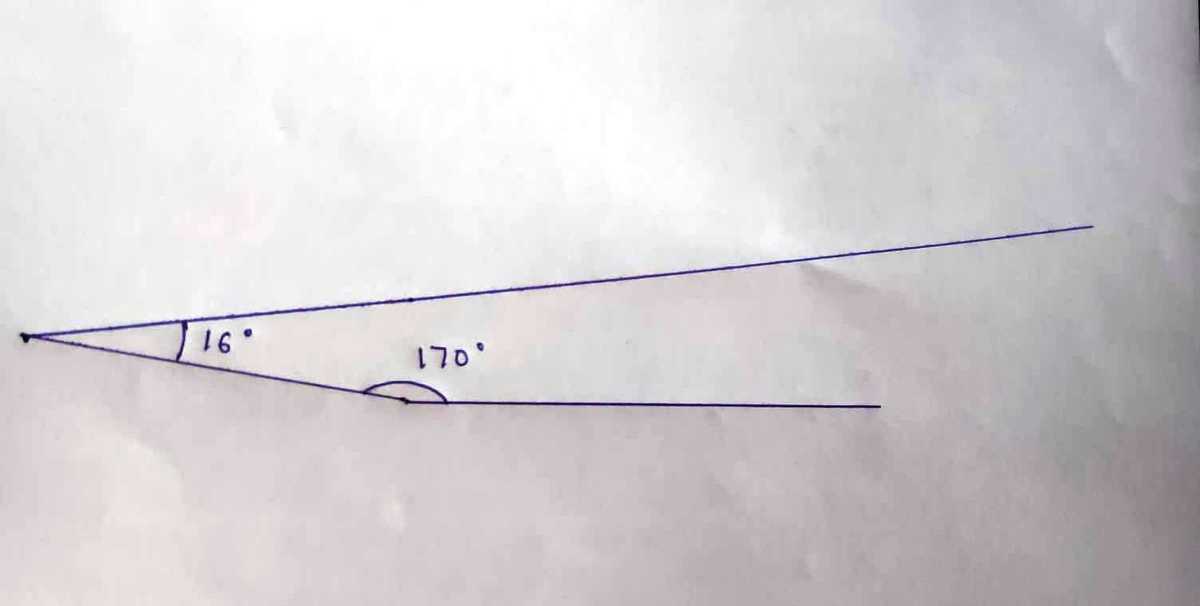
I have a question : how can an angle be -6 degree?...Can you explain it?....In case of your solution, everything is clear understandable...But my common sense says Y can't be 54 degree..Am i correct?

Md. Mubin Hasan - 2 years, 1 month ago

Yes, you are correct. X and Y must be greater than 60 degrees and the sum of X and Y must be smaller than 300. I have edited my answer. Thank you for pointing the mistake.

Adrash singh - 2 years, 1 month ago

what a solution !

Vinish Kumar - 2 years, 1 month ago

Mind your decision it's amazing

Nitin Upadhyay - 1 year, 4 months ago

Nice and easy solution

Hiviru Palihena - 11 months, 2 weeks ago

YuJin Kim
Feb 18, 2019

I asked myself two questions.

[Question 1] Can you determine the angles of a triangle if you know the lengths of its sides?
[Question 2] Can you determine the lengths of the specified segments?

I believe, but can't really prove that both of the questions are answered by a "yes." If we were to assume so, we do know the angles of our new triangle.

I have a question. How do you know if question 2 gets a "yes"?

MegaMoh .
Sep 10, 2020

the locus of all points $A$ such that angle $SAR= x$ is a part of a circle(you can imagine it as an inscribed angle in a circle, the part before crossing the subtended chord) which can intersect other similar circle-part shapes in at most 2 points. Drawing that locus on $SR$ for $x$ and $QR$ for $y$ , there intersection is the point P(meaning where it is possible to have an angle $SPR=x$ and $QPR=y$ ) and since they already have a common point $R$ , there is only 1 more possible point of intersection therefore it unique there the lengths of $PS$ , $PQ$ , and $PR$ are unique therefore we can find the angles by SSS.

Transforming Triangle

4 solutions

0 pending reports