Transient vs. Steady State (4-16-2021)
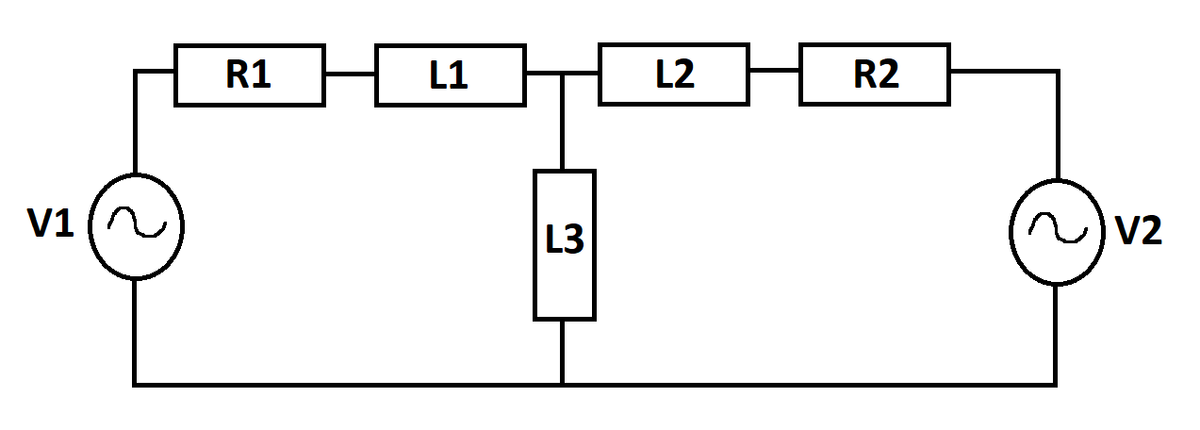
An R L circuit is excited by two A C voltage sources as shown. At time t = 0 , the inductors are de-energized. Let I 3 ( t ) be the current flowing in inductor L 3 . Let I 3 S S ( t ) be a pure sinusoid such that I 3 ( t ) and I 3 S S ( t ) become the same signal after initial transients subside.
Determine the following integral:
Q = ∣ ∣ ∣ ∫ 0 ∞ ( I 3 ( t ) − I 3 S S ( t ) ) d t ∣ ∣ ∣
Details and Assumptions:
1)
V
1
(
t
)
=
1
0
2
sin
(
t
+
π
/
4
)
volts
2)
V
2
(
t
)
=
7
2
sin
(
t
)
volts
3)
R
1
=
R
2
=
0
.
2
5
Ω
4)
L
1
=
L
2
=
L
3
=
1
H
The answer is 75.74.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Nicely done!
Wow, what a great question! :D I'm learning transient analysis currently in my electrical engineering course. This was really fun to solve. Here, I labelled the currents as follows.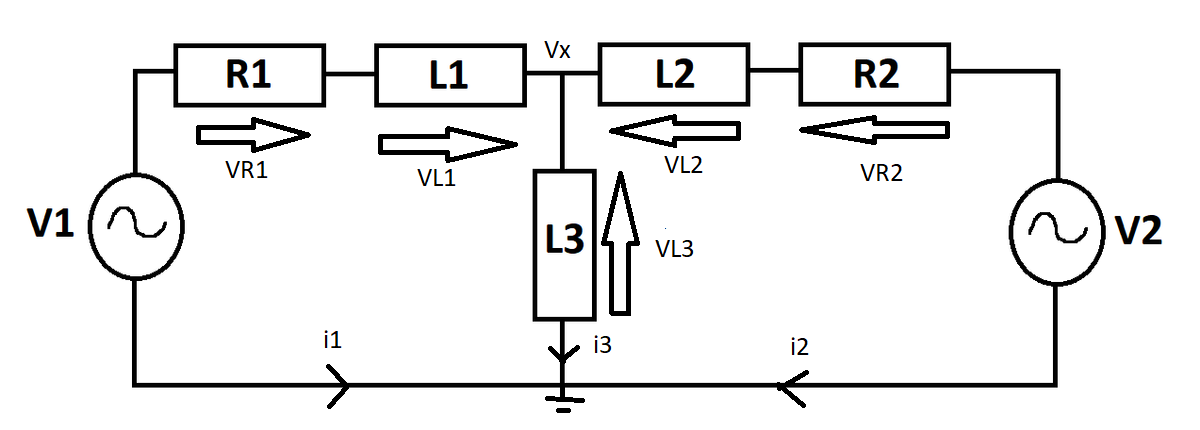
By KCL, i 1 + i 2 + i 3 = 0 . We can also formulate equations based on the voltages in the circuit. Firstly, V R 1 = i 1 R 1 V R 2 = i 2 R 2 V L 1 = L 1 d t d i 1 V L 2 = L 2 d t d i 2 V L 3 = L 3 d t d i 3 Using the node voltage V x : V x = V 1 + i 1 R 1 + L 1 d t d i 1 ( 1 ) V x = V 2 + i 2 R 2 + L 2 d t d i 2 ( 2 ) V x = L 3 d t d i 3 ( 3 ) Adding these three equations while substituting in the resistances and inductances gives: 3 V x = V 1 + V 2 + 0 . 2 5 − i 3 ( i 1 + i 2 ) + d t d i 1 + d t d i 2 + d t d i 3 Due to the linearity of the derivative: d t d i 1 + d t d i 2 + d t d i 3 = d t d 0 ( i 1 + i 2 + i 3 ) = 0 Furthermore, the V x in our equation is simply d t d i 3 via equation ( 3 ) . Thus, 3 d t d i 3 = V 1 + V 2 − 0 . 2 5 i 3 3 d t d i 3 + 0 . 2 5 i 3 = V 1 + V 2 This is a first order, linear, non-homogeneous ODE. Let's first find the homogeneous part of the solution. Using the trial solution method: 3 λ + 0 . 2 5 = 0 ⟶ λ = 3 − 0 . 2 5 = 1 2 − 1 So the complementary solution is i 3 c ( t ) = A e − 1 2 t .
Now we need to find the particular solution, i 3 p ( t ) . To do this, first simplify the RHS. sin ( t + 4 π ) = sin ( t ) cos ( 4 π ) + cos ( t ) sin ( 4 π ) = 2 sin ( t ) + cos ( t ) V 1 ( t ) + V 2 ( t ) = 1 0 ( sin ( t ) + cos ( t ) ) + 7 2 sin ( t ) = ( 1 0 + 7 2 ) sin ( t ) + 1 0 cos ( t ) This is in the form a sin ( t ) + b cos ( t ) , so this will be our 'guess' for i 3 p ( t ) . Then i 3 p ′ ( t ) = a cos ( t ) − b sin ( t ) . Substituting this into our ODE: 3 ( a cos ( t ) − b sin ( t ) ) + 4 a sin ( t ) + b cos ( t ) = ( 1 0 + 7 2 ) sin ( t ) + 1 0 cos ( t ) Equating coefficients: 4 a − 3 b = 1 0 + 7 2 3 a + 4 b = 1 0 ( 4 1 3 − 3 4 1 ) ( a b ) = ( 1 0 + 7 2 1 0 ) ( a b ) = ( 4 1 3 − 3 4 1 ) − 1 ( 1 0 + 7 2 1 0 ) = 9 + 1 6 1 1 ( 4 1 − 3 3 4 1 ) ( 1 0 + 7 2 1 0 ) = ( 3 . 8 5 9 − 6 . 3 1 2 ) Therefore, i 3 ( t ) = A e − 1 2 t + 3 . 8 5 9 sin ( t ) − 6 . 3 1 2 cos ( t ) The energy stored in the inductors is modelled by E = 2 1 L i 2 where i is the current through it. This means that when the inductors are de-energized at t = 0 , i 1 = i 2 = i 3 = 0 since L = 0 . Consequently, i 3 ( 0 ) = 0 . 0 = A e 0 + 3 . 8 5 9 sin ( 0 ) − 6 . 3 1 2 cos ( 0 ) ⟶ A = 6 . 3 1 2 i 3 ( t ) = transient 6 . 3 1 2 e − 1 2 t + ’steady state’ 3 . 8 5 9 sin ( t ) − 6 . 3 1 2 cos ( t ) The transient part is as such because as t → ∞ , it goes to zero, while the steady state part doesn't. This makes sense because the homogeneous solution is always the transient while the steady state part the particular solution. The steady state part is precisely I 3 S S ( t ) .
Now, we are finally ready to solve the integral. The integrand is simply the complementary solution i 3 c ( t ) = 6 . 3 1 2 e − 1 2 t . Q = ∫ 0 ∞ 6 . 3 1 2 e − 1 2 t d t = 6 . 3 1 2 × − 1 2 × e − 1 2 t ∣ ∣ ∣ 0 ∞ = 1 2 × 6 . 3 1 2 = 7 5 . 7 4