Trapdoor Problem
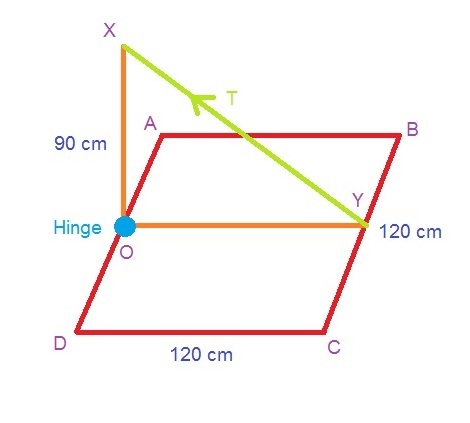 A trapdoor 120 cm by 120 cm is kept horizontal by a string attached to the midpoint of the side opposite to that containing the hinge. The other end of the string is tied to a point 90 cm vertically above the hinge. If the weight of the trapdoor is 50 Newtons, what is the tension in the string, in Newtons?
A trapdoor 120 cm by 120 cm is kept horizontal by a string attached to the midpoint of the side opposite to that containing the hinge. The other end of the string is tied to a point 90 cm vertically above the hinge. If the weight of the trapdoor is 50 Newtons, what is the tension in the string, in Newtons?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
(120-90) then i calculated for cos30*9.8 and then multiplied by gravity.at Last subtract 50-8.48=41.5
Write a comment or ask a question... good
3T/5 * 1.2 = 50 * 0.6 .......... 6T = 250 ........... T = 41.67 N
Write a comment or ask a qunice estion...
equate the vertical components of the torque due to the thread and the weight of doortrap about the point of hinge...
T 3/5 120=50*60
force balance due to Tension "T" in the string and the weight "W", 1st we calculate the angle made by string from vertical,i.e, tan(theta)=90/120 =36.87 degree from horizontal or 90-36.87=53.13 degree from vertical. Therefore, Now take moment about hinge to be zero; (Tcos (theta)]120}-{50*(weight=60)=0; =41.67 N
the anticlockwise torque about O= clockwise torque about O. ie. T sin 37degree * 1.2 Nm= 50 * 0.6 Nm
right bt method u r using is wrong we have consider both x n y diracted forces
VERY NICE QUESTION ABID BHAI...MAJA AA GAYA. REGARDS ANURAG TYAGI CLASSES (ATC)
NOTE: here we can not apply balancing of forces in vertical or horizontal directions as we dont know the reaction forces at hinge. so do it by conservation of angular momentum
how is weight is 60??????
Moment at hinge is equal to zero.The center of weight is located at the middle .By taking summation of moment at hinge is equal to zero .You will determine tension of the string.0= 50 newtonx 60cm- Tsin36.870 x 120cm. One equation and one unknown you will solve the tension. Tension is 41.667 newton
Write a comment or ask a question... v.nice
Its a Basic Problem from elementary mechanics,i.e, Torque balancing or you may call it a simple force balance due to Tension "T" in the string and the weight "W", Therefore 1st we have to calculate the angle made by string from vertical,i.e, tan(theta)=90/120 => theta=tan^-1(3/4)=36.87 degree from horizontal or 90-36.87=53.13 degree from vertical. Therefore, Now take moment about hinge to be zero; =>{ [T cos(theta)] 120}-{50*(weight=60)}=0; =>T=41.67 N
Can you explain where does weight=60 comes from ?
Log in to reply
Weight is 50 newton and 60 cm is distance of centre of mass
You can get from my solution@Rafail Yousaf
Write a comment or ask a question.good..
to lift the trapdoor ..which rotates about the Hinge ..we need to overcome the roating effect due to WEIGHT..about the hinge... so balnce the torque due to tension..... with torque due to weight about hinge...THAT will BE just enough force to lift it up
Write a comment or ask a question... best
considering the moment about O ..Tsin theta * 1.2 = mg * 0.6 mg = 50N and sin theta = 3/5.. on solving this equation we get T= 41.67N
i am not understanding this please help me to understand this
Tau=tsin@ r=mg r' r=1.2 for hinge to string pt.... r'=0.6 till the com of door....
Write a comment or ask a question... good
Consider the rotational equilibrium about point O.
Write a comment or ask a question... v.v.good
Take the moment at the hinge , but before you do that find the angle by tan@= 90/120, @= 36.87, then find the moments about the hinge to find reaction
Who knows how To find reaction at hinge
balance the moment of tension and weight about the hinge. t(9/15)(12)=(50)(6)