Trapezium

Geometry Level 3

The A B C D ABCD is trapezium, where A B ∣ ∣ C D AB\mid\mid CD and A B = 2 ∗ C D AB=2*CD . The F F point divides the A D AD side to two equal parts. The A C , B F , B D AC, BF, BD segments form the colored triangles.

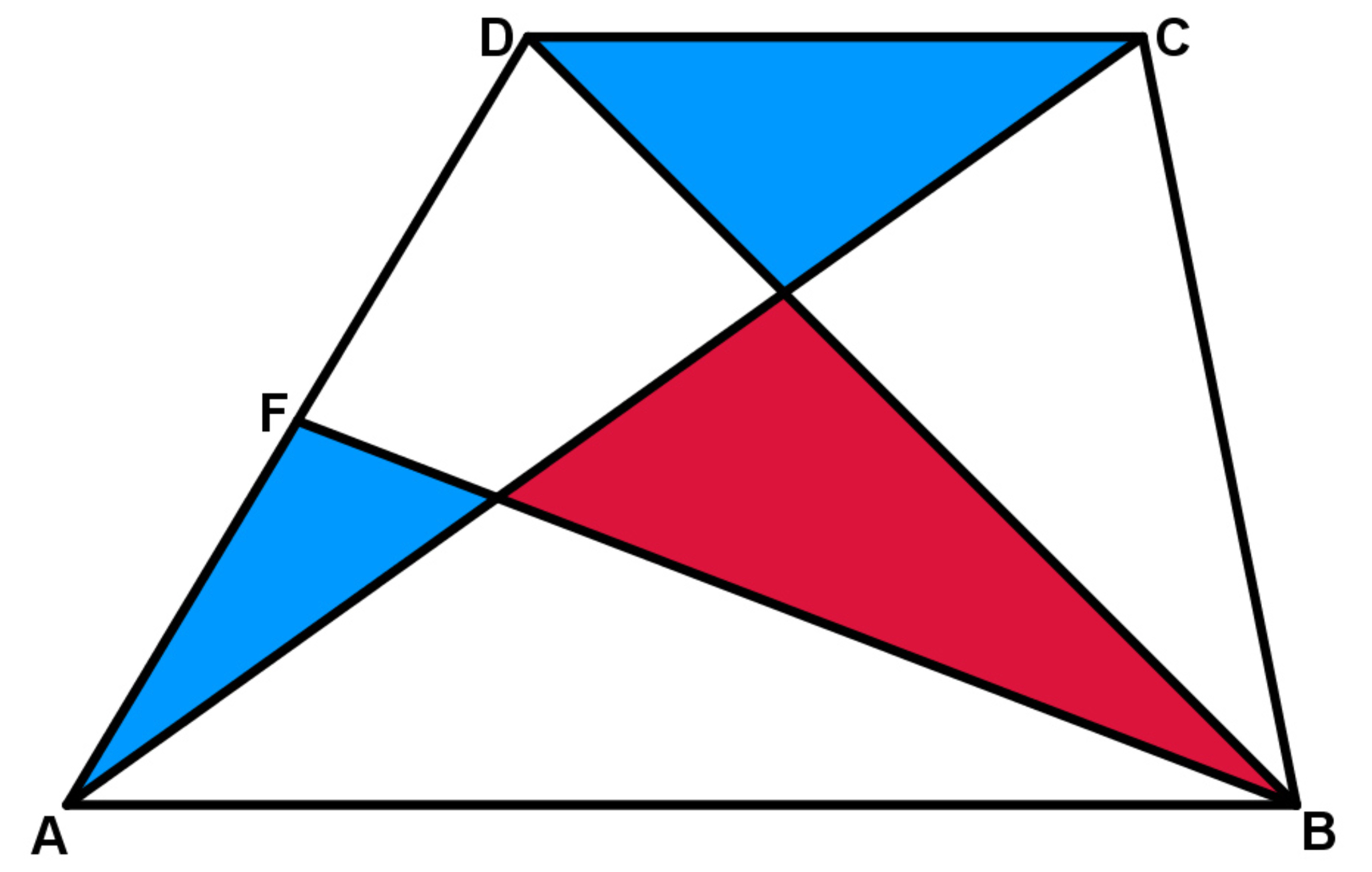
Which area is larger, the red or the blue?

They are equal The blue area The red area Can't be determined

Áron Bán-Szabó by Áron Bán-Szabó , 17, Hungary

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Áron Bán-Szabó
Jul 11, 2017

Complete the trapezoid to the A B G D ABGD parallelogram. [ B F D ] = 1 2 [ A B D ] = 1 4 [ A B G D ] [BFD]=\dfrac{1}{2}[ABD]=\dfrac{1}{4}[ABGD] [ D A C ] = 1 2 [ D A G ] = 1 4 [ A B G D ] [DAC]=\dfrac{1}{2}[DAG]=\dfrac{1}{4}[ABGD] The equations above can be seen in the figure. As a consequence, [ B F D ] = [ A D C ] [BFD]=[ADC] . By subtract [ E F G D ] [EFGD] we get red area = sum of the areas of the blue triangles \text{red area}=\text{sum of the areas of the blue triangles}

3 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...