Trapezium Artists
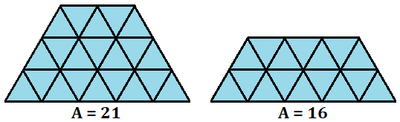
Using unit equilateral triangular tiles, you can construct the following trapezoids with areas of 2 1 and 1 6 :
Find the sum of all the integer areas between 1 0 0 and 2 0 0 that can not be constructed from trapezoids made from unit equilateral triangular tiles.
Note: in this question, parallelograms are not considered trapezoids.
The answer is 3750.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Side note: trapezoid or trapezium? And don't parallelograms count? (This appears to be a bit of a minefield)
Log in to reply
Nice solution! I edited the problem to clarify that parallelograms do not count as trapezoids and to add a wikipedia link for trapezoids. Thanks for the feedback!
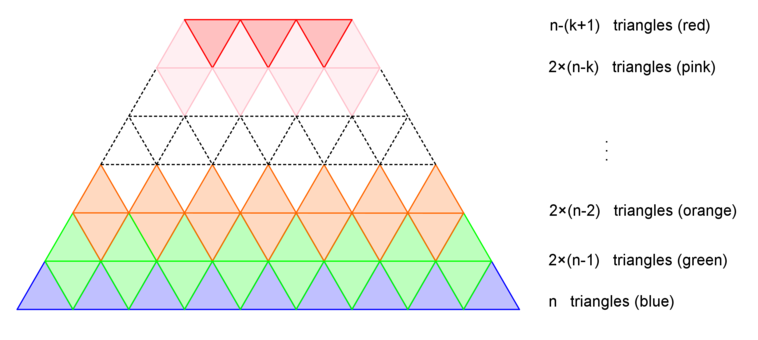 Just to verify the claim that the number of triangles in any trapezium is the difference of the squares of the lengths of the trapezium’s bases, we add
Just to verify the claim that the number of triangles in any trapezium is the difference of the squares of the lengths of the trapezium’s bases, we add
n + 2 ( n − 1 ) + 2 ( n − 2 ) + … + 2 ( n − k ) + ( n − ( k + 1 ) ) = k + 1 terms 2 n + 2 n + … + 2 n − 2 ( 1 + 2 + … + k ) − ( k + 1 ) = 2 n ( k + 1 ) − 2 2 k ( k + 1 ) − ( k + 1 ) = ( k + 1 ) ( 2 n − k − 1 ) = [ n − ( n − ( k + 1 ) ) ] [ n + ( n − ( k + 1 ) ) ] = n 2 − ( n − ( k + 1 ) ) 2
Obvious restrictions for integers n and k : n ≥ 2 , 0 ≤ k ≤ n − 2 .
The rest is best explained by @Chris Lewis .
This is very good! I got a bit confused about the observation @Chris Lewis arrived at, but this explains all. Both solutions are good!
The possible trapeziums have areas of the difference between two perfect squares (because the nth layer counting from the top of this triangle corresponds to the nth triangular number, and the first n of them sum up to n²), so the impossible areas should be even numbers between 100 and 200 that are not divisible by 4.
Sum of impossible areas
= (100 / 4) × (102 + 198) / 2
= 3750
We can make a valid configuration with any odd number of equilateral triangles by extending this pattern: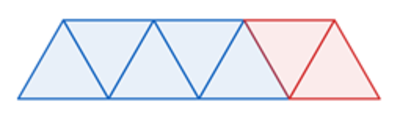
We can get any multiple of four with this pattern: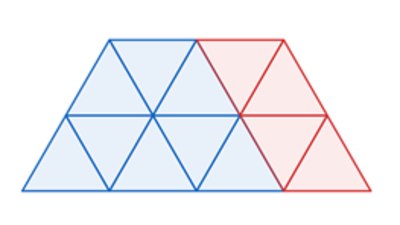
In general, note that the number of triangles in one of these shapes is the difference of the squares of the lengths of the parallel sides; for instance, 2 1 = 5 2 − 2 2 and 1 6 = 5 2 − 3 2 .
All square numbers are either of the form 4 k or 4 k + 1 ; so the difference of two squares can never be of the form 4 k + 2 .
So the areas we can't make are 1 0 2 , 1 0 6 , 1 1 0 , … , 1 9 8 , whose total (found by summing the arithmetic progression) is 3 7 5 0 .