Trapezoid
 If
O
A
,
O
B
,
O
C
,
O
D
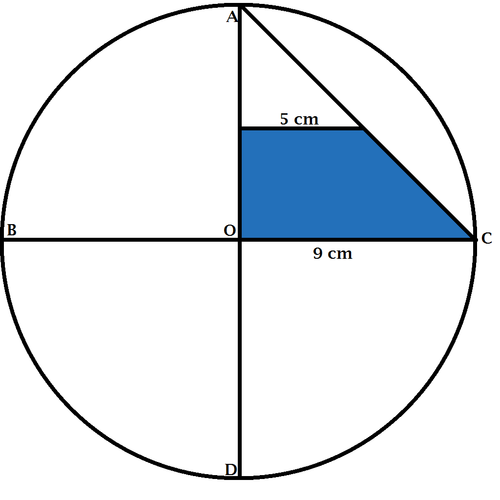
are the radii of this circle then find the area of the trapezoidal shape in blue.
If
O
A
,
O
B
,
O
C
,
O
D
are the radii of this circle then find the area of the trapezoidal shape in blue.
The answer is 28.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
This problem assumes that the 5 cm line is parallel to OC. Once you figure out that that is true, the problem is easy, but if you assume that they are parallel, you cannot complete the problem. The problem should be revised to say that they are parallel.
Yes, I know the title is trapezoid, but but the problem should reflect that.
Log in to reply
Thanks, I've added it in.
Log in to reply
Oh, and how do you report a problem once you have already answered the question?
It is not necessary to say they are parallels because it is a trapezoid, so they are parallels.
I have assumed that without knowing it was not specified.
Dear Friend, It is a right angled Trapezoid.
I see someone said that the problem has been revised, did it not describe the blue region as trapezoidal when you wrote that?
You should specify upper triangle is right angle triangle as it cant be guess.
Log in to reply
I think it was possible to solve despite the triangle is not specified. You can use cartesian coordinate system. Take the OA and OC as the axis, O is the origin, and AC is a line x+y=9. So, when you put x=5, you get y=4.
The Difference between the Area of triangle AOC and Area of triangle AEF is the Area of The Blue Shaded region.
It's the difference of the areas of two isosceles right triangles, 2 9 × 9 − 2 5 × 5 = 2 8
Is AO PERPENDICULAR to BC?
if AO . CO are radii that means AO=OC the area=9 9 0.5-5 5 0.5 // // =28cm^2
let the line equivalent to 5cm be BT Therefore; Triangle AOC ||| Triangle ABT(similar) AO/AB = OC/BT 9/AB =9/5 9AB=45 AB =5cm BO=9-5 BO=4 AREA OF TRAPEZOIDAL=1/2 *(9+5) * 4 =28cm2
In the problem it has been mentioned that the shaded area is trapezoidal.
Since it is a trapezoid two sides has to be parallel.
Therefore the smaller triangle and triangle AOC are similar.
If the triangles are similar, the corresponding sides are proportional.
Hence we get one side of the trapezium as 4 cm.
Since one more side is known the trapezium can be splitted as a rectangle of area 5*4 sq cm and a right angled triangle with height 4cm and base 4 cm
Adding the area of the rectangle and that of the triangle gives the total area of the trapezium I.e,
Area of trapezium in sq cm= (5 * 4)+(1/2 * 4 * 4)= 28 sq cm
Also this applies if AO is perpendicular to OC
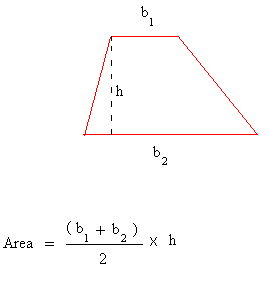
In the above figure, we note that △ A E F is similar to △ A O C and A E = E F = 5 c m .
Therefore, O E = 9 − 5 = 4 c m .
Then, the area of the b l u e -shaded region is = 2 5 + 9 × 4 = 2 8 c m 2 .