Trapezoid and areas
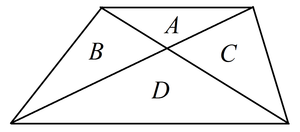 The trapezoid is divided by the diagonals into four triangles with areas
,
,
, and
.
The trapezoid is divided by the diagonals into four triangles with areas
,
,
, and
.
If , what is ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Label the figure as follows.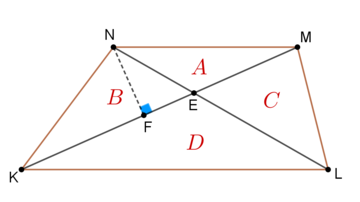 △
N
K
E
and
△
N
E
M
share a common altitude,
N
F
, thus, the ratio of their areas equals the ratio of the corresponding bases:
A
B
=
E
M
K
E
⇒
E
M
K
E
=
3
△
E
K
L
and
△
E
M
N
are similar (alternating angles), hence the ratio of their areas equals the square of their similarity ratio, i.e.
A
D
=
(
E
M
K
E
)
2
Combining,
A
D
=
3
2
⇒
D
=
9
A
△
N
K
E
and
△
N
E
M
share a common altitude,
N
F
, thus, the ratio of their areas equals the ratio of the corresponding bases:
A
B
=
E
M
K
E
⇒
E
M
K
E
=
3
△
E
K
L
and
△
E
M
N
are similar (alternating angles), hence the ratio of their areas equals the square of their similarity ratio, i.e.
A
D
=
(
E
M
K
E
)
2
Combining,
A
D
=
3
2
⇒
D
=
9
A