Trapezoid Area
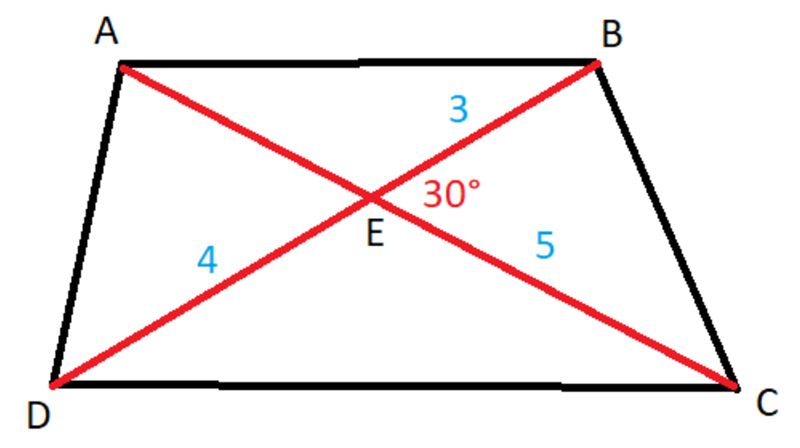
In trapezoid A B C D the two diagonals A C and B D intersect at point E . If B E = 3 , C E = 5 , D E = 4 , and ∠ B E C = 3 0 ∘ , then the area of the trapezoid can be written as b a for coprime positive integers a and b . Enter the value of the sum a + b .
The answer is 261.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
From the given informations we have
∣ A B ∣ = 4 3 ∣ C D ∣ ,
tan ∠ B A C = 5 + 2 3 2
Using these we get the height of the trapezoid as h = 2 4 1 + 2 0 3 3 5 ,
and ∣ A B ∣ + ∣ C D ∣ = 4 7 × 4 1 + 2 0 3
So, the required area of the trapezoid is
2 1 × 4 7 4 1 + 2 0 3 × 2 4 1 + 2 0 3 3 5
= 1 6 2 4 5
So, a = 2 4 5 , b = 1 6 , and a + b = 2 4 5 + 1 6 = 2 6 1 .
We note that △ A B E and △ C D E are similar. Then B E A E = D E C E ⟹ A E = D E C E × B E = 4 5 × 3 = 4 1 5 . The area of trapezoid A B C D is
[ A B C D ] = 2 1 A E ⋅ B E sin ∠ A E B + 2 1 D E ⋅ A E sin ∠ D E A + 2 1 C E ⋅ D E sin ∠ C E D + 2 1 B E ⋅ C E sin ∠ B E C = 2 1 ⋅ 4 1 5 ⋅ 3 ⋅ sin 1 5 0 ∘ + 2 1 ⋅ 4 ⋅ 4 1 5 ⋅ sin 3 0 ∘ + 2 1 ⋅ 5 ⋅ 4 ⋅ sin 1 5 0 ∘ + 2 1 ⋅ 3 ⋅ 5 ⋅ sin 3 0 ∘ = 1 6 4 5 + 4 1 5 + 5 + 4 1 5 = 1 6 2 4 5
Therefore a + b = 2 4 5 + 1 6 = 2 6 1 .