Trapezoid Area from Slant Mid-Bridge
is a trapezoid with the following properties:
- is the distance between and
- is the midpoint of while is the midpoint of
Find the area of trapezoid
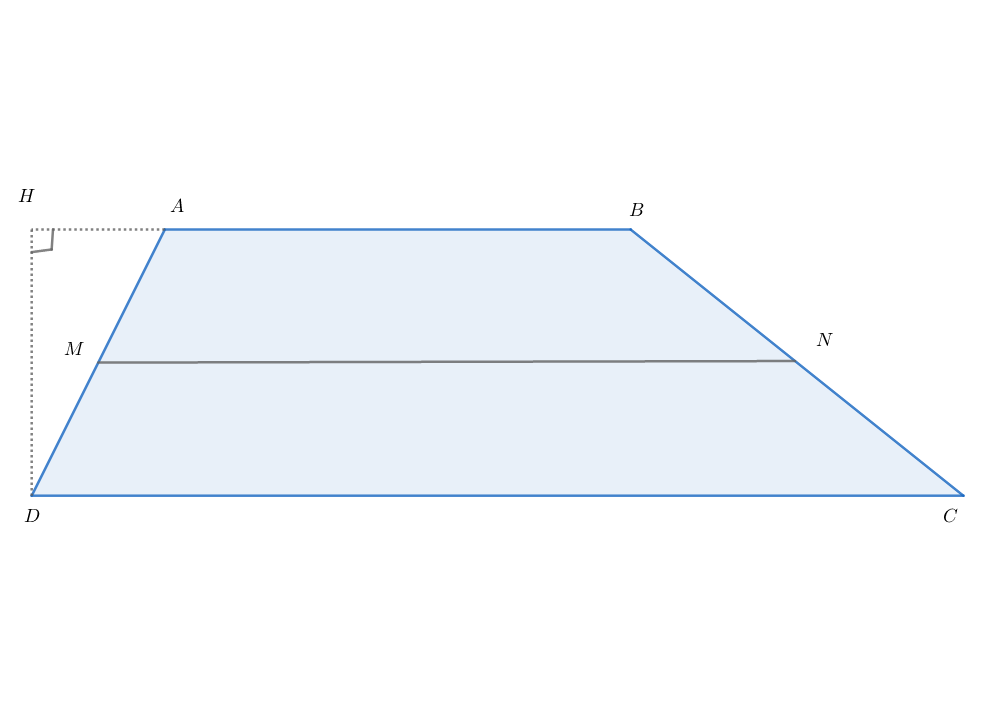
The answer is 2018.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
I took the trapezium, copied it, rotated it 180 degrees and stuck them together by the side BC:
Placing angle ABC adjacent to angle BCD gives a straight line, as the two angles are co-interior on the parallel lines AB and DC, and co-interior angles add to 180 degrees.
The resulting shape AEFD is a parallelogram, as the opposite angles are equal. This means that the left and right sides are also equal, so their midpoints would be equivalent, i.e.
A M = M D = E O = O F
This means that the quadrilaterals AEOM and MOFD are also parallelograms, and since opposite sides in a parallelogram are equal:
A E = M O
But since MO consists of two copies of MN, and AE consists of the lines AB and CD stuck together,
A B + C D = 2 M N
= 2 × 1 0 0 9
= 2 0 1 8
Now we can use the rule for the area of a trapezium:
A r e a = 2 h ( a + b ) where a and b are the parallel sides and h is the perpendicular height.
A r e a = 2 H D ( A B + C D )
= 2 2 ( 2 0 1 8 )
= 2 0 1 8